Personalita' ricreative - Maurice Kraitchik

Biografia

Maurice Kraitchik (21 Aprile 1882 Minsk – 19 Agosto 1957 Bruxelles), è stato un matematico belga e divulgatore scientifico.
I suoi principali interessi sono stati la teoria dei numeri e la matematica ricreativa.

Kraitchik è nato in Russia, dove ha studiato fino al 1903.
In seguito, per via delle restrizioni sugli studi per gli Ebrei, si è trasferito in Belgio, a Liegi.
Qui si è laureato nel 1910 presso l'Università statale (ULG) come ingegnere elettrico. Successivamente, a causa della prima guerra mondiale, non potè ritornare in Russia e accettò l'incarico di ingegnere presso una società finanziaria belga, la Société Financière de Transports et d'Entreprises Industrielles (Sofina), dove rimase fino al suo pensionamento, avvenuto nel 1948.
Nel 1923 ha conseguito il dottorato presso l'Université libre de Bruxelles (ULB) in matematica (teoria dei numeri).
Dopo aver ricevuto il dottorato, in qualità di professore associato, ha tenuto lezioni sulla teoria dei numeri presso l'Università di Bruxelles. E 'stato poi direttore dell'Institut des Hautes Etudes de Belgique. Kraitchik ha scritto diversi libri sulla teoria dei numeri tra il 1922 e il 1930.
Dal 1931 al 1939 è stato il direttore di Le Sphinx, una rivista mensile dedicata alla matematica ricreativa¹.

Nel 1935 ha organizzato a Bruxelles il primo congresso internazionale sulla matematica ricreativa, a cui è seguita una seconda conferenza nel 1937 a Parigi.
Durante la seconda guerra mondiale (1941-1946), Kraitchik emigrò negli Stati Uniti, dove ha insegnato alla New School for Social Research di New York, sul tema generale delle ricreazioni matematiche. Nel 1941 entrò a far parte della MAA, partecipando, tra l'altro, a vari meeting estivi in quegli anni.

Tra i vari risultati ottenuti, Kraitchik ha migliorato nel 1926 il metodo di fattorizzazione di Pierre de Fermat, con un'idea che sarà poi alla base del successivo crivello quadratico di Pomerance.
Ha poi ideato anche una formula per il calcolo del giorno della settimana di una data nel calendario Gregoriano².

Infine è noto per aver ideato un problema analogo al successivo e famoso paradosso delle due buste (two envelopes problem) (vedi più giù).

Le sue principali pubblicazioni a carattere matematico sono:

• Théorie des Nombres, Parigi: Gauthier-Villars, 1922
• Recherches sur la théorie des nombres, Parigi: Gauthier-Villars, 1924
• La mathématique des jeux ou Récréations mathématiques, Parigi: Vuibert, 1930, 566 pages
• Mathematical Recreations, New York: W. W. Norton, 1942, 328 pagine (2nd edition New York: Dover, 1953)

Libri e opere di matematica ricreativa

Il primo libro a carattere ricreativo pubblicato da Kraitchik è La mathématique des jeux ou Récréations mathématiques.
Il libro di ben 566 pagine, è in francese.
Il secondo è più conosciuto libro di matematica ricreativa è Mathematical Recreations, che in sostanza è una versione rivista e compattata del primo.
Mathematical Recreations è stato pubblicato per la prima volta nel 1942 da W. W. Norton. Ci fu poi una edizione britannica nel 1955 e la ben nota Dover edition nel 1953, con ulteriori editioni nel 1981 e nel 2006.
Ad eccezione di alcuni cambiamenti, riconoscibili per via di un differente stile, il contenuto attuale è praticamente lo stesso dell'edizione originale del 1942. Il libro si divide in dodici capitoli che danno una buona idea del contenuto.
Tra questi vi sono problemi antichi e curiosi, passatempi numerici, probabilità, quadrati magici, ricreazioni geometriche, giochi e molto altro.

Il gioco del Tricolor

Il Tricolor è un gioco di pura strategia inventato da Kraitchik e descritto per la prima volta nel libro "La Mathématique des Jeux"³.
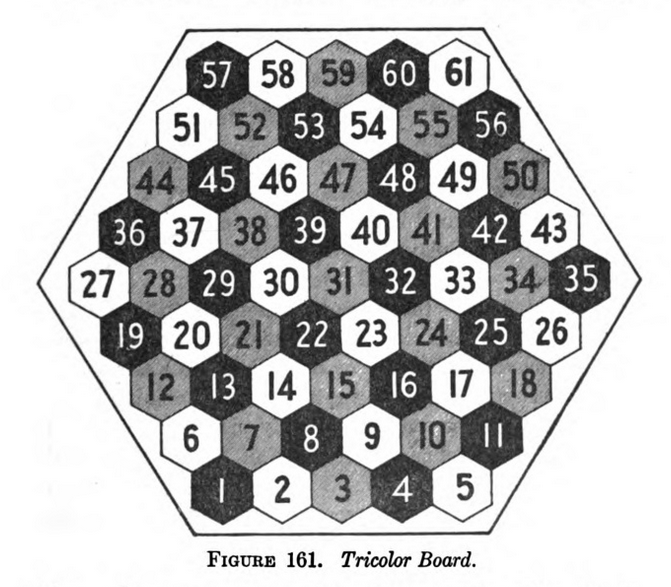
Si tratta di uno dei più datati giochi del tipo ad impilare, simile al Lasca. Viene giocato su di una scacchiera esagonale, con le caselle colorate di bianco, rosso e nero, in modo tale che due caselle adiacenti non hanno mai lo stesso colore (vedi immagine di seguito).
Così come il Lasca, il Tricolor viene giocato con pile di una o più pedine, ma le pile sono libere di muoversi in una qualsiasi delle tre o sei direzioni di uscita da una casella.
Il range di una pila di pedine - definito come il massimo numero di caselle che la pila può attraversare in una unica direzione e con una sola mossa - è determinato dal numero di pedine che compongono la pila: 1 casella per una singola pedina, 2 caselle per una pila di 2 pedine, e 3 caselle per un pila di 3 o più pedine.

Indicando con l'unità la forza di combattimento di una singola pedina su di una casella bianca, si ha che la strength di una pila formata da 2 pedine su di una casella bianca è di 2 unità, quella di una pila di 3 o più pedine su di una casella bianca è di 3 unità.
La forza di una pila su di una casella nera è 2 volte la forza della stessa pila su una casella bianca, mentre la forza di una pila su di una casella rossa è pari a 3 volte quella della stessa pila su di una casella bianca.
Ragion per cui la forza di una pila è sempre rappresentata da uno dei numeri 1, 2, 3, 4, 6, 9.
Il gioco a due giocatori. Ciascun giocatore ha a disposizione 18 pedine. Bianche per un giocatore, nere per l'altro. Quando il gioco inizia, Il bianco ha le sue pedine posizionate selle caselle dalla 1 alla 18. Il nero similarmente ha le sue pedine posizionate dalla 44 alla 61 (vedi Fig.4).
I giocatori giocano a turno, ciascuno muovendo una singola pila (o pedina) di un numero qualsiasi di caselle, purchè rientri nel range della pila, lungo una linea retta in una delle direzioni permesse.
Un giocatore può muovere tutta la pila o solo una parte, ma il range e la forza della pila è determinata dal numero di pedine presenti nella parte della pila che viene effettivamente mossa.
Non può saltare caselle occupate. Può posizionarsi su di una casella vuota, su di una casella occupata da una propria pila, oppure (vedi le regole per l'attacco) su di una casella occupata da una pila avversaria di energia più bassa.
Se la casella di destinazione contiene una propria pila, le due pile vengono combinate a formare un'unica pila.
Se la casella di destinazione è occupata da una pila avversaria, allora si dice che il giocatore ha attaccato una pila avversaria, e la disposizione delle pedine viene stabilita secondo le regole di attacco di seguito esposte.
Una pila, può attaccare una pila avversaria solo se la sua forza di combattimento è maggiore di quella avversaria. Se tale forza è maggiore più del doppio, la pila avversaria viene "mangiata" rimuovendo da essa tutte le pedine nemiche, ed aggiungendovi tutte le pedine amiche. Le pedine così aggiunte vanno ad incrementare il range e la forza della pila attaccante, se possibile.
Se la pila attaccante è più forte dell'avversaria, ma non più del doppio, la pila avversaria viene "catturata", combinandola con la pila attaccante. In questo caso solo le pedine amiche vengono conteggiate nella determinazione del range e della forza della pila risultante.
Se un attacco è possibile, deve essere fatto, e il giocatore che attacca è libero di scegliere uno qualsiasi degli attacchi a disposizione.
Non più di un attacco può essere fatto in un singolo turno.
Il gioco termina con la rimozione o la cattura di tutte le pedine avversarie.
Il gioco a tre giocatori. Ciascun giocatore ha a disposizione 11 pedine colorate rispettivamente di bianco, nero e rosso.
Inizialmente le pedine biance sono posizionate sulle caselle da 1 a 11; le nere sulle caselle 19,27,28,36,37,44,45,51,52,57,58; e le rosse sulle caselle 60, 61, 55, 56, 49, 50, 42, 43, 34, 35, 26 (vedi Fig.4).
Giocano a turno, prima il Bianco, poi il Nero ed infine il Rosso.
Le regole sono le stesse che per il gioco a 2 giocatori, eccetto che per il finale. In pratica, quando tutte le pedine di un giocatore sono state rimosse o catturate, egli si ritira dal gioco, le sue rimanenti pedine vengono rimosse dalla scacchiera e la partita continua a 2 giocatori.

Alcuni problemi interessanti estratti dai libri

Il paradosso delle cravatte

Each of two persons claims to have the finer necktie. They call in a third person who must make a decision. The winner must give his necktie to the loser as consolation. Each of the contestants reasons as follows: "I know what my tie is worth. I may lose it, but I may also win a better one, so the game is to my advantage". How can the game be to the advantage of both? The question can be put in an arithmetical form. Two people agree that they will compare the number of pennies in their purses, and that the one who has the greater number must give them all to the other. In case of a tie, no money is transferred.

che tradotto è pressappoco così:

Due persone sostengono ciascuno di avere una cravatta più costosa di quella dell'altro. Così, per decidere chi dei due avesse ragione viene chiamata una terza persona che dovrà prendere la decisione. Il vincitore darà la sua cravatta al perdente in segno di consolazione. Ora le due persone possono ragionare entrambe allo stesso modo, ossia: "So che la mia cravatta è di valore. Posso perderla, ma posso anche vincerne una migliore". Così il paradosso è, com'è possibile che il gioco sia vantaggioso per entrambe le parti? La questione può essere posta in forma aritmetica. Ossia due persone concordano nel confrontare il numero di monete nei loro portamonete, e che chi possiede il maggior numero di monete, dovrà cederle all'altro. In caso di parità nessuna moneta viene trasferita.

Il problema risale al 1930, ed è presente nel libro La mathématique des jeux, in lingua francese ⁴.
Viene successivamente riproposto in inglese, nel libro Mathematical Recreations del 1953, nella versione di cui sopra ⁵.
Nel 1982 Martin Gardner ha reso popolare il rompicapo nella versione con i portamonete (noto come The Wallet paradox), proponendolo nel suo libro Aha! Gotcha⁶. Nel 1989 Barry Nalebuff lo ha presentato nella forma delle due buste e, da allora, questa è la forma più comunemente usata: il famoso paradosso delle due buste.
Kraitchik, analizzando il problema nella versione con i portamonete, propone una soluzione grafica che mostra agevolmente come la situazione sia equa e quindi non ci sia vantaggio per alcuno dei partecipanti.
Tuttavia, come fa notare Gardner, egli non fornisce alcuna spiegazione sul perchè il ragionamento dei due giocatori sia errato.
Una possibile risposta a questa domanda viene fornita da David S.Ross ⁷.

Riferimenti bibliografici

• Maurice Kraitchik, Mathematical Recreations, 2nd edition, Dover, New York, 1953.
• Maurice_Kraitchik - Wikipedia DE
• MAA - Mathematical Recreations