
Bene, :) concluso il primo post sulle pile di Gergonne, mi erano rimasti ancora dei dubbi su alcuni aspetti della procedura di generalizzazione proposta nel paper di J.Harrison et al. 1
Inoltre mancava una parte molto interessante, ossia capire come poter applicare praticamente la formula del paper alle possibili varianti del gioco.
Pertanto eccoci al secondo episodio.
Ulteriore analisi sulla generalizzazione
Riprendiamo il caso denominato Periodic column recollection case (vedi qui).
Ricapitolando, in questo caso viene analizzata la situazione più generale in cui ad ogni ricomposizione $i$ la pila scelta viene riposta in una qualsiasi posizione $k_i$ con $0\le k_i \le p-1$.
In pratica viene utilizzata l'idea di pattern periodico, ossia viene considerato un insieme di $m$ ricomposizioni e ridistribuzioni, che viene ripetuto periodicamente.
Il pattern nello specifico ci è dato dalle $m$ posizioni $k_i$ in cui viene riposta la pila in ogni ricomposizione.
Pertanto in questo caso $\ell$ sta ad indicare la periodicità, ossia il numero di volte che viene rieseguito il pattern.
L'analisi porta alla seguente formula, che ci da appunto la posizione finale della carta nella pila scelta, dopo $\ell$ ripetizioni del pattern:
dove
con $1\le x \le n$; con $0 \le k \le p-1$ e con $n\ge 2$.
Vediamo praticamente cosa significa ciò.
Supponiamo di considerare un numero $p$ di pile formate da $n$ carte ciascuna (per cui un totale di $n*p$ carte), e di eseguire il gioco.
Supponiamo di effettuare un numero $m$ di ricomposizioni (le distribuzioni saranno $m+1$), dove ad ogni $i-esima$ ricomposizione la pila scelta viene riposta in posizione $k_i$,
e di ripetere il tutto $\ell$ volte.
Ebbene al termine del procedimento, dopo l'ultima ridistribuzione (la $m+1$esima), dopo che lo spettatore avrà indicato la pila contenente la carta da lui scelta all'inizio,
saremo in grado di conoscere la posizione di detta carta nella pila, grazie alla formula di cui sopra.
Tale posizione ci sarà data da $\left\lfloor L \right\rfloor -1$ nel caso in cui $L$ è intero e se la posizione $x$ della carta scelta dallo spettatore risulta inferiore ad $L$.
In tutti gli altri casi la posizione finale ci sarà data da $\left\lfloor L \right\rfloor$.
Per cui, ad esempio, supponiamo di eseguire il gioco con $4$ pile di $8$ carte ciascuna, e che lo spettatore inizialmente sceglie la carta in posizione $4$ di una pila.
Ora supponendo di ottenere un $L=5$ al termine del procedimento, essendo verificata la condizione $x<L$ la posizione finale della carta ci sarà data da $\left\lfloor L \right\rfloor -1$.
Valore di $\ell$ e validità della formula
Harrison et al. nel loro articolo ci dicono che la formula di cui sopra risulta valida per
In realtà tale valore di soglia per $\ell$ è solo una approssimazione per eccesso del valore di soglia reale e ciò comporta una sovrastima del valore di $\ell$ in alcuni casi.
Tuttavia ai fini del nostro gioco, ci interessa di trovare sempre il valore intero più basso per $\ell$ per il quale la formula risulta valida,
valore che ci garantirebbe il minor numero di ridistribuzioni e ricomposizioni.
Ad esempio per $\ell=8$ la formula risulta sicuramente valida, ma non ha senso rieseguire $8$ volte la stessa sequenza di operazioni, quanto magari basterebbe farlo solo $1$ volta.
Pertanto abbiamo bisogno del valore reale di soglia (che indichiamo per comodità con $V_s$).
Seguendo sempre le indicazioni del paper, si può ricavare tale valore di soglia in funzione di $x$. Si ha (vi risparmio i calcoli):
dove $\widetilde{r}$ è il resto della divisione intera tra $\sum_{i=1}^{m}{k_inp^{i-1}+p^m-1}$ e $p^m-1$.
A noi, come detto, interessa il valore di $\ell$ per cui la formula risulta valida sempre, indipendentemente da $x$.
Per cui dobbiamo metterci nel caso peggiore, ossia considerare il valore massimo tra tutti i possibili valori di $V_s(x)$.
La formula dunque risulterà sempre valida per $\ell > max\lbrace V_s(x) \rbrace$.
Quindi il più piccolo valore intero di $\ell$ che verifica la disuguaglianza, sarà quello da utilizzare per il nostro gioco.
Applicazione della formula alle possibili varianti del gioco
Anzitutto definiamo un caso di gioco (o configurazione).
Un caso di gioco è ogni possibile esecuzione del gioco, con $n$, $p$, $m$ ed $\ell$ fissati.
Ad esempio l'esecuzione del gioco con $4$ pile di $8$ carte ciascuna, con $2$ ricomposizioni, ed $1$ solo esecuzione del pattern, rappresenta un possibile caso di gioco (ossia il caso $8x4$).
Premesso ciò, vediamo come è possibile applicare praticamente la formula ai casi di gioco.
Si nota che, quando eseguiamo il gioco, ovviamente non sappiamo la posizione $x$ (nella pila) della carta scelta inizialmente dallo spettatore (altrimenti il gioco non avrebbe senso).
Ciò potrebbe far pensare che la formula quindi non sia applicabile, per via della condizione $x<L$ in essa presente.
In realtà vi sono vari casi in cui la condizione risulta vera o falsa, indipendentemente dal valore di $x$; ad esempio quando $L$ è intero ed è pari a $1$ oppure è pari ad $n+1$.
E sono proprio questi casi che funzionano bene per il nostro gioco.
Vediamo ora, come individuare tali casi "magici".
Si tratta sostanzialmente di scegliere un caso di gioco da valutare, ed analizzarlo manualmente.
In pratica, all'interno di una configurazione di gioco, possiamo avere diversi scenari, a seconda delle diverse posizioni in cui viene riposta di volta in volta la pila scelta,
ossia a seconda dei valori $\lbrace k_1,k_2,…,k_m\rbrace$.
Per cui affinchè il caso in questione risulti "magico", c'è bisogno che per ogni diversa combinazione di valori $\lbrace k_1,k_2,…,k_m\rbrace$ si ottenga un valore di $L$ non intero,
oppure un valore intero pari a $1$ o $n+1$.
Proviamo ad analizzare ad esempio la configurazione di gioco con $n=8$, $p=5$, $m=2$, $l=1$.
Analisi del caso di gioco 8x5
Calcoliamo per ogni possibile combinazione $\lbrace k_1,k_2\rbrace$ i valori di $L$ e $max\lbrace V_s(x) \rbrace$.
Essendo tali calcoli un tantino noiosi da farsi manualmente, ho realizzato un piccolo programma al pc 2 che li esegue per noi.
Otteniamo la seguente tabella:
| $\lbrace k_1,k_2\rbrace$ | $L = \displaystyle\frac{\sum_{i=1}^{m}{k_i\cdot n\cdot p^{i-1}}}{p^m-1}+1$ | $f^l(x)$ | $\ell > max\lbrace V_s(x) \rbrace$ |
|---|---|---|---|
| $\lbrace 0,0\rbrace$ | 1 | 1 | 0,557 |
| $\lbrace 0,1\rbrace$ | 2,667 | 2 | 0,797 |
| $\lbrace 0,2\rbrace$ | 4,333 | 4 | 0,715 |
| $\lbrace 0,3\rbrace$ | 6 | 6 o 5 | 0,5 |
| $\lbrace 0,4\rbrace$ | 7,667 | 7 | 0,715 |
| $\lbrace 1,0\rbrace$ | 1,333 | 1 | 0,665 |
| $\lbrace 1,1\rbrace$ | 3 | 3 o 2 | 0,431 |
| $\lbrace 1,2\rbrace$ | 4,667 | 4 | 0,605 |
| $\lbrace 1,3\rbrace$ | 6,333 | 6 | 0,861 |
| $\lbrace 1,4\rbrace$ | 8 | 8 o 7 | 0,605 |
| $\lbrace 2,0\rbrace$ | 1,667 | 1 | 0,861 |
| $\lbrace 2,1\rbrace$ | 3,333 | 3 | 0,605 |
| $\lbrace 2,2\rbrace$ | 5 | 5 o 4 | 0,431 |
| $\lbrace 2,3\rbrace$ | 6,667 | 6 | 0,665 |
| $\lbrace 2,4\rbrace$ | 8,333 | 8 | 0,96 |
| $\lbrace 3,0\rbrace$ | 2 | 2 o 1 | 0,5 |
| $\lbrace 3,1\rbrace$ | 3,667 | 3 | 0,715 |
| $\lbrace 3,2\rbrace$ | 5,333 | 5 | 0,797 |
| $\lbrace 3,3\rbrace$ | 7 | 7 o 6 | 0,557 |
| $\lbrace 3,4\rbrace$ | 8,667 | 8 | 0,759 |
| $\lbrace 4,0\rbrace$ | 2,333 | 2 | 0,605 |
| $\lbrace 4,1\rbrace$ | 4 | 4 o 3 | 0,341 |
| $\lbrace 4,2\rbrace$ | 5,667 | 5 | 0,605 |
| $\lbrace 4,3\rbrace$ | 7,333 | 7 | 0,915 |
| $\lbrace 4,4\rbrace$ | 9 | 8 | 0,646 |
Si nota anzitutto che il valore più alto di $max\lbrace V_s(x) \rbrace$ si ha per la configurazione $\lbrace 2,4\rbrace$ ed è pari a $0,96$.
Ciò significa che prendendo $l=1$ la formula risulterà valida per ogni configurazione $\lbrace k_1,k_2\rbrace$.
Per quanto riguarda $L$, osserviamo che in corrispondenza delle configurazioni $\lbrace 0,3\rbrace$,$\lbrace 1,1\rbrace$,$\lbrace 1,4\rbrace$,$\lbrace 2,2\rbrace$,
$\lbrace 3,0\rbrace$,$\lbrace 3,3\rbrace$,$\lbrace 4,1\rbrace$ abbiamo dei valori di $L$ interi, diversi da $1$ ed $n+1$.
Ciò significa che per tali configurazioni non è possibile determinare con esattezza la posizione finale della carta scelta.
Pertanto il caso in questione non è "magico" 3.
Analizziamo adesso un caso magico, ossia il caso $8\text{x}6$.
Analisi del caso di gioco 8x6
Consideriamo la configurazione di gioco con $n=8$, $p=6$, $m=2$, $l=1$.
Sempre con l'aiuto del software simulatore si ottiene la seguente tabella:
| $\lbrace k_1,k_2\rbrace$ | $L = \displaystyle\frac{\sum_{i=1}^{m}{k_i\cdot n\cdot p^{i-1}}}{p^m-1}+1$ | $f^l(x)$ | $\ell > max\lbrace V_s(x) \rbrace$ |
|---|---|---|---|
| $\lbrace 0,0\rbrace$ | 1 | 1 | 0,5 |
| $\lbrace 0,1\rbrace$ | 2,371 | 2 | 0,557 |
| $\lbrace 0,2\rbrace$ | 3,743 | 3 | 0,709 |
| $\lbrace 0,3\rbrace$ | 5,114 | 5 | 1 |
| $\lbrace 0,4\rbrace$ | 6,486 | 6 | 0,677 |
| $\lbrace 0,5\rbrace$ | 7,857 | 7 | 0,58 |
| $\lbrace 1,0\rbrace$ | 1,229 | 1 | 0,562 |
| $\lbrace 1,1\rbrace$ | 2,6 | 2 | 0,669 |
| $\lbrace 1,2\rbrace$ | 3,971 | 3 | 1,301 |
| $\lbrace 1,3\rbrace$ | 5,343 | 5 | 0,709 |
| $\lbrace 1,4\rbrace$ | 6,714 | 6 | 0,58 |
| $\lbrace 1,5\rbrace$ | 8,086 | 8 | 1,232 |
| $\lbrace 2,0\rbrace$ | 1,457 | 1 | 0,648 |
| $\lbrace 2,1\rbrace$ | 2,829 | 2 | 0,891 |
| $\lbrace 2,2\rbrace$ | 4,2 | 4 | 0,774 |
| $\lbrace 2,3\rbrace$ | 5,571 | 5 | 0,58 |
| $\lbrace 2,4\rbrace$ | 6,943 | 6 | 0,514 |
| $\lbrace 2,5\rbrace$ | 8,314 | 8 | 0,878 |
| $\lbrace 3,0\rbrace$ | 1,686 | 1 | 0,789 |
| $\lbrace 3,1\rbrace$ | 3,057 | 3 | 1 |
| $\lbrace 3,2\rbrace$ | 4,429 | 4 | 0,58 |
| $\lbrace 3,3\rbrace$ | 5,8 | 5 | 0,5 |
| $\lbrace 3,4\rbrace$ | 7,171 | 7 | 1 |
| $\lbrace 3,5\rbrace$ | 8,543 | 8 | 0,734 |
| $\lbrace 4,0\rbrace$ | 1,914 | 1 | 1,139 |
| $\lbrace 4,1\rbrace$ | 3,286 | 3 | 0,58 |
| $\lbrace 4,2\rbrace$ | 4,657 | 4 | 0,536 |
| $\lbrace 4,3\rbrace$ | 6,029 | 6 | 1,443 |
| $\lbrace 4,4\rbrace$ | 7,4 | 7 | 0,774 |
| $\lbrace 4,5\rbrace$ | 8,771 | 8 | 0,645 |
| $\lbrace 5,0\rbrace$ | 2,143 | 2 | 0,58 |
| $\lbrace 5,1\rbrace$ | 3,514 | 3 | 0,55 |
| $\lbrace 5,2\rbrace$ | 4,886 | 4 | 0,814 |
| $\lbrace 5,3\rbrace$ | 6,257 | 6 | 0,842 |
| $\lbrace 5,4\rbrace$ | 7,629 | 7 | 0,657 |
| $\lbrace 5,5\rbrace$ | 9 | 8 | 0,58 |
Si nota in questo caso che il valore più alto di $max\lbrace V_s(x) \rbrace$ si ha per la configurazione $\lbrace 4,3\rbrace$ ed è pari a $1,443$.
Ciò significa che dobbiamo prendere $\ell=2$ affinchè la formula risulterà valida per ogni configurazione $\lbrace k_1,k_2\rbrace$.
Per quanto riguarda $L$, osserviamo che si ha un solo valore intero, pari a $9$ (ossia $n+1$), in corrispondenza della configurazione $\lbrace 5,5\rbrace$.
Pertanto il caso in questione risulta "magico", a condizione che vengano effettuate $\ell=2$ iterazioni, ognuna formata da $2$ ricomposizioni, per un totale di $4$ ricomposizioni.
In realtà, in questo caso è interessante notare che, se aumentiamo il numero di ricomposizioni $m$ da $2$ a $3$, il caso resta "magico" però con $\ell=1$;
per cui con un totale di $3$ ricomposizioni, rispetto alle $4$ della configurazione precedente.
Analisi di altri casi al simulatore
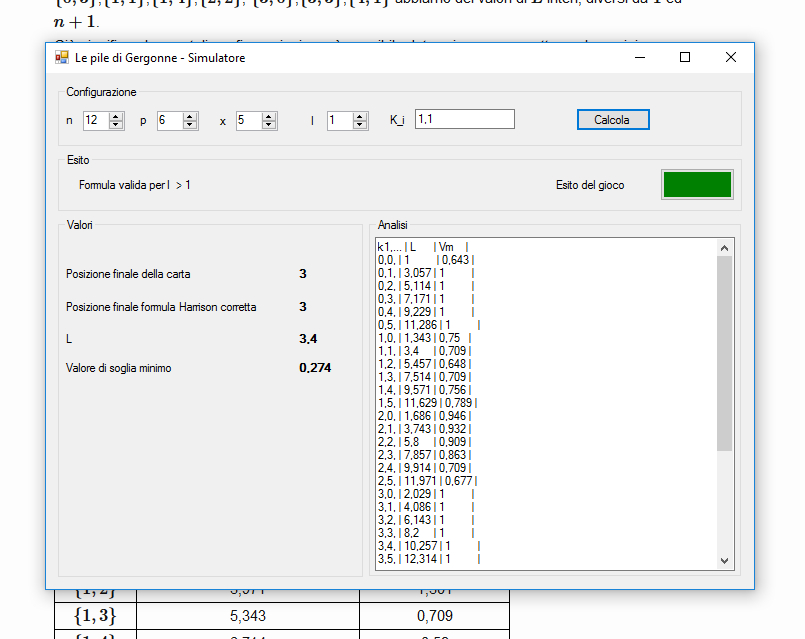
Il software di simulazione delle pile di gergonne, prende in input i parametri $n$, $p$, $x$, $\ell$, ed i valori delle posizioni $k_i$, separati da virgola (ad es. $1$,$1$,$3$ nel caso di $3$ ricomposizioni)
e ci ritorna la posizione finale effettiva della carta, la posizione finale secondo la formula di Harrison, il valore specifico di L, ed il valore minimo di soglia.
Inoltre, utilizzando i soli valori di input $n$, $p$, ed il numero $m$ di posizioni $k_i$, fornisce i valori di $L$ e $max\lbrace V_s(x) \rbrace$ per ogni combinazione di posizioni, e ci dice se il caso sia "magico" o meno,
tramite una etichetta colorata (verde o rossa).
Ebbene, giocando con i parametri di input si possono trovare facilmente i casi "magici".
Alcuni sono i seguenti:
- caso $9\text{x}3$ - $n=9$, $p=3$, $m=2$, $\ell=1$
- caso $9\text{x}6$ - $n=9$, $p=6$, $m=2$, $\ell=1$
- caso $8\text{x}4$ - $n=8$, $p=4$, $m=2$, $\ell=1$
- caso $8\text{x}6$ - $n=8$, $p=6$, $m=2$, $\ell=2$
- caso $8\text{x}6$ - $n=8$, $p=6$, $m=3$, $\ell=1$
- caso $10\text{x}4$ - $n=10$, $p=4$, $m=3$, $\ell=2$
- caso $12\text{x}6$ - $n=12$, $p=6$, $m=2$, $\ell=1$
Chiaramente nel caso di $2$ iterazioni, la seconda iterazione va effettuata utilizzando le stesse posizioni $k_i$ scelte nella prima iterazione.
Semplificazione della formula
Nel primo post sull'argomento abbiamo visto che la posizione finale della carta, ci era data, nel caso $9\text{x}3$ dalla formula
mentre nel caso $8\text{x}4$ era
Si nota come entrambe le formule siano più semplici della formula $\eqref{a}$ vista finora. Come si spiega ciò?
Bene, ciò è possibile grazie al fatto che in questi due casi particolari la formula $\eqref{a}$, può essere approssimata dalla seguente
che altro non è che il valore di $L$ senza però il $-1$ al denominatore.
Infatti, consideriamo ad es. la seguente tabella per il caso $9\text{x}3$:
| $\lbrace k_1,k_2\rbrace$ | $L = \displaystyle\frac{\sum_{i=1}^{m}{k_i\cdot n\cdot p^{i-1}}}{p^m-1}+1$ | $f^l(x)$ | $L_2 = \displaystyle\frac{\sum_{i=1}^{m}{k_i\cdot n\cdot p^{i-1}}}{p^m}+1$ | $\left\lfloor L_2\right\rfloor$ |
|---|---|---|---|---|
| $\lbrace 0,0\rbrace$ | 1 | 1 | 1 | 1 |
| $\lbrace 0,1\rbrace$ | 4,375 | 4 | 4 | 4 |
| $\lbrace 0,2\rbrace$ | 7,75 | 7 | 7 | 7 |
| $\lbrace 1,0\rbrace$ | 2,125 | 2 | 2 | 2 |
| $\lbrace 1,1\rbrace$ | 5,5 | 5 | 5 | 5 |
| $\lbrace 1,2\rbrace$ | 8,875 | 8 | 8 | 8 |
| $\lbrace 2,0\rbrace$ | 3,25 | 3 | 3 | 3 |
| $\lbrace 2,1\rbrace$ | 6,625 | 6 | 6 | 6 |
| $\lbrace 2,2\rbrace$ | 10 | 9 | 9 | 9 |
comparando le due formule si nota come $f^l(x)$ ed $\left\lfloor L_2\right\rfloor$ siano equivalenti per ciascun scenario.
Pertanto, possiamo utilizzare $\left\lfloor L_2\right\rfloor$ nel caso $9\text{x}3$.
Si ottiene
che ci da la posizione della carta nella pila dopo la seconda distribuzione.
Solitamente però viene effettuata una ulteriore ricomposizione (superflua) del mazzo, con la pila in oggetto che viene rimessa in posizione $k_3$.
Dopo di che la carta scelta viene indovinata contando $n_c$ carte a partire dalla cima del mazzo così ricomposto.
Per questo al valore di cui sopra va aggiunto il termine $9\cdot k_3$, ottenendo quindi
che è proprio la formula semplificata cercata. Lo stesso vale per il caso $8\text{x}4$.
Quindi, una volta individuato un caso magico, possiamo provare a semplificare la formula, tramite l'utilizzo di $L_2$.
Ovviamente, affinchè sia possibile qualche semplificazine, c'è bisogno che $n$ e $p$ abbiamo dei divisori in comune.
Proviamo con un nuovo caso.
Abbiamo visto al simulatore che il caso $9\text{x}6$ risulta essere magico.
Dato che $9$ e $6$ hanno dei divisori in comune, proviamo a semplificare la formula finale.
Ricaviamo la tabella con i valori di $L$, $f^l(x)$, e $L_2$ per ogni possibile scenario:
| $\lbrace k_1,k_2\rbrace$ | $L = \displaystyle\frac{\sum_{i=1}^{m}{k_i\cdot n\cdot p^{i-1}}}{p^m-1}+1$ | $f^l(x)$ | $L_2 = \displaystyle\frac{\sum_{i=1}^{m}{k_i\cdot n\cdot p^{i-1}}}{p^m}+1$ | $\left\lfloor L_2\right\rfloor$ |
|---|---|---|---|---|
| $\lbrace 0,0\rbrace$ | 1 | 1 | 1 | 1 |
| $\lbrace 0,1\rbrace$ | 2,543 | 2 | 2,5 | 2 |
| $\lbrace 0,2\rbrace$ | 4,086 | 4 | 4 | 4 |
| $\lbrace 0,3\rbrace$ | 5,629 | 5 | 5,5 | 5 |
| $\lbrace 0,4\rbrace$ | 7,171 | 7 | 7 | 7 |
| $\lbrace 0,5\rbrace$ | 8,714 | 8 | 8,5 | 8 |
| $\lbrace 1,0\rbrace$ | 1,257 | 1 | 1,25 | 1 |
| $\lbrace 1,1\rbrace$ | 2,8 | 2 | 2,75 | 2 |
| $\lbrace 1,2\rbrace$ | 4,343 | 4 | 4,25 | 4 |
| $\lbrace 1,3\rbrace$ | 5,886 | 5 | 5,75 | 5 |
| $\lbrace 1,4\rbrace$ | 7,429 | 7 | 7,25 | 7 |
| $\lbrace 0,5\rbrace$ | 8,971 | 8 | 8,75 | 8 |
| $\lbrace 2,0\rbrace$ | 1,514 | 1 | 1,5 | 1 |
| $\lbrace 2,1\rbrace$ | 3,057 | 3 | 3 | 3 |
| $\lbrace 2,2\rbrace$ | 4,6 | 4 | 4,5 | 4 |
| $\lbrace 2,3\rbrace$ | 6,143 | 6 | 6 | 6 |
| $\lbrace 2,4\rbrace$ | 7,686 | 7 | 7,5 | 7 |
| $\lbrace 2,5\rbrace$ | 9,229 | 9 | 9 | 9 |
| $\lbrace 3,0\rbrace$ | 1,771 | 1 | 1,75 | 1 |
| $\lbrace 3,1\rbrace$ | 3,314 | 3 | 3,25 | 3 |
| $\lbrace 3,2\rbrace$ | 4,857 | 4 | 4,75 | 4 |
| $\lbrace 3,3\rbrace$ | 6,4 | 6 | 6,25 | 6 |
| $\lbrace 3,4\rbrace$ | 7,943 | 7 | 7,75 | 7 |
| $\lbrace 3,5\rbrace$ | 9,486 | 9 | 9,25 | 9 |
| $\lbrace 4,0\rbrace$ | 2,029 | 2 | 2 | 2 |
| $\lbrace 4,1\rbrace$ | 3,571 | 3 | 3,5 | 3 |
| $\lbrace 4,2\rbrace$ | 5,114 | 5 | 5 | 5 |
| $\lbrace 4,3\rbrace$ | 6,657 | 6 | 6,5 | 6 |
| $\lbrace 4,4\rbrace$ | 8,2 | 8 | 8 | 8 |
| $\lbrace 4,5\rbrace$ | 9,743 | 9 | 9,5 | 9 |
| $\lbrace 5,0\rbrace$ | 2,286 | 2 | 2,25 | 2 |
| $\lbrace 5,1\rbrace$ | 3,829 | 3 | 3,75 | 3 |
| $\lbrace 5,2\rbrace$ | 5,371 | 5 | 5,25 | 5 |
| $\lbrace 5,3\rbrace$ | 6,914 | 6 | 6,75 | 6 |
| $\lbrace 5,4\rbrace$ | 8,457 | 8 | 8,25 | 8 |
| $\lbrace 5,5\rbrace$ | 10 | 9 | 9,75 | 9 |
La formula $L_2$ risulta essere equivalente a $f^l(x)$ per questo caso, per cui possiamo utilizzarla.
Pertanto la formula finale, nel caso di un ulteriore ultima ricomposizione del mazzo, sarà:
Si nota come questa formula sia decisamente più semplice di quella ottenuta con la formula $\eqref{a}$, ossia:
Bene, comincio a pensare che per tutti i casi "magici" si possa utilizzare la formula $L_2$ …
Riferimenti bibliografici
- W. W. Rouse Ball, Mathematical Recreations and Essays, 12th edition, New York, 1975.
- Joseph Diaz Gergonne - Wikipedia IT
-
J. Harrison, T. Brennan, and S. Gapinski, The Gergonne p-pile problem and the dynamics of the function x → (x + r)/p, Discrete Applied Mathematics 82 (1998) 103–113 ↩
-
Il software è disponibile sotto licenza GPL, e ne trovate la versione eseguibile nella sezione progetti del sito. Il codice sorgente invece è disponibile su Github. ↩
-
Chiaramente il caso potrebbe essere comunque reso magico facendo attenzione ad evitare, durante l'esecuzione del gioco, gli scenari non buoni. ↩






