Anamorfosi floreale

Ogni anno, in occasione della solennità del Corpus Domini, nel mio paesino, ha luogo l'infiorata, manifestazione consistente nel realizzare quadri e tappeti floreali, lungo le strade, e nelle piazze e chiese del posto. Quest'anno, per il ventennale dell'evento, abbiamo deciso di cimentarci nella realizzazione di un quadro un pò fuori dagli schemi classici: un quadro anamorfico floreale. E' stato un esperimento, ed avevamo più di un dubbio sulla riuscita dello stesso; ma a giudicare dal risultato e dal riscontro di pubblico, direi che ce la siamo cavata bene! :P

Di seguito alcune foto che mostrano l'illusione ottica:

Le foto ingannano, ma come si può intuire dalle ultime due foto, il disegno si estende per  ben 9 metri in altezza e 7 metri in larghezza. 

Di seguito tutti i nomi della banda di "matti" che ha concepito e realizzato l'opera:

Pietro Vitelli, Giuseppe Vitelli, Giuseppe Crocco, Antonio Iadarola, Michele Iadarola, Carlo Vitelli, Emilio Vitelli, Fred Di Biase, Paolo Franco, Marino Di Gennaro, Federico Petrillo, Giovanni Civitillo

Ma veniamo alla parte teorica…

Cos'è l'anamorfosi?

Prendendo a prestito la definizione di Wikipedia, l'anamorfismo è un effetto di illusione ottica per cui una immagine viene proiettata sul piano in modo distorto, rendendo il soggetto originale riconoscibile solamente guardando l'immagine da una posizione ben precisa. Per capirci, sono esempi di anamorfosi i cartelloni pubblicitari presenti ai lati delle porte dei campi di calcio, che vediamo sovente in tv o allo stadio.

Conosciuta anche con il nome di "prospettiva inversa", questa tecnica comincia ad essere utilizzata ed approfondita intorno al XV secolo, con Leonardo Da Vinci e Piero Della Francesca.

Famoso è il quadro Gli Ambasciatori di Hans Holbein il Giovane, nella cui parte bassa è presente un piccolo teschio deformato, riconoscibile solo osservando il dipinto in scorcio di lato.

Ancor più famoso ed imponente è invece l'affresco realizzato da Andrea Pozzo nella chiesadi S.Ignazio di Loyola in Campo Marzio a Roma.

Maggiori e più dettagliate informazioni sono disponibili nell'interessante rapporto tecnico dell'ENEA sull'argomento.

Attualmente la tecnica anamorfica viene utilizzata abilmente da molti artisti, tra i quali troviamo Julian Beever, Kurt Wenner, Leon Keer, Edgar Muller  ed altri, che hanno realizzato opere anamorfiche di grande impatto visivo sulle strade e sui muri di varie città del mondo.

Nonostante ciò, poche sono le informazioni reperibili su carta e/o in rete sulle tecniche e metodi utili alla realizzazione di disegni anamorfici. Un documento di riferimento in tal senso è il trattato La perspective curieuse di Jean Francois Niceron,  in cui viene esposto un metodo grafico dal quale è possibile partire per deformare un disegno "normale", per ottenere l'effetto anamorfico.

Ed è proprio da qui che siamo partiti per realizzare il nostro disegno anamorfico di cui sopra.

Metodo e formule per la realizzazione di un disegno anamorfico

Consideriamo la costruzione grafica riportata nel trattato di Niceron, ossia le due figure XXXVIII e XXXIX:

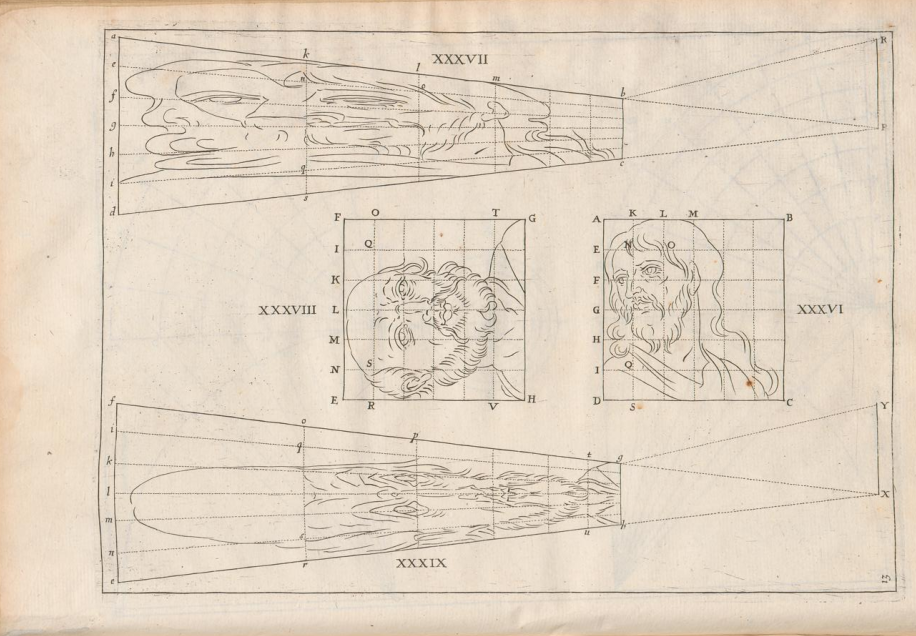
In pratica l'immagine di cui si vuole ottenere l'effetto anamorfico viene deformata, allargandola agli angoli superiori ed allungandola, in una sorta di prospettiva "a contrario", di modo tale che, guardandola in prospettiva "naturale", si annullino queste deformazioni, e compaia il disegno originale. Intuitivamente ciò è abbastanza semplice da capire; meno semplice è stabilire l'entità della deformazione in funzione della posizione da cui si vuole osservare il quadro. A tale scopo, consideriamo la seguente versione più dettagliata della costruzione di Niceron:

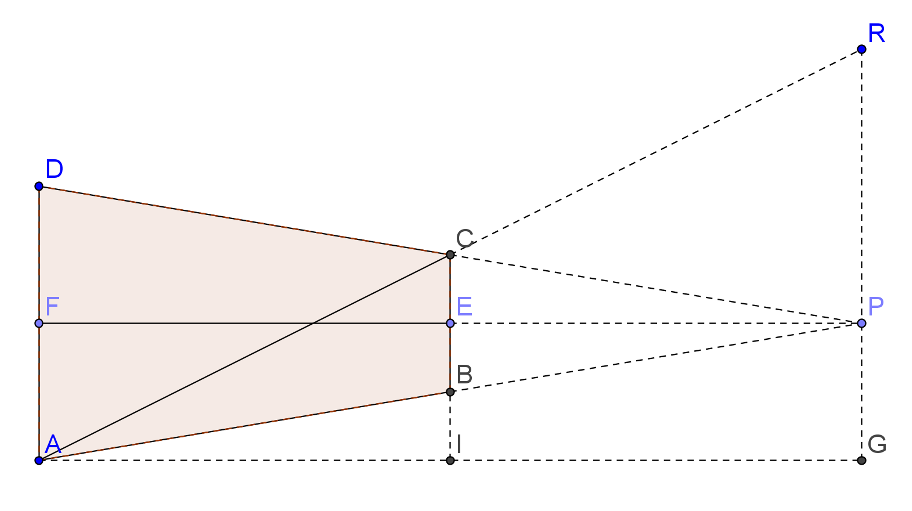
Le regole prospettiche ci dicono che il punto $P$ è il punto di fuga delle linee verticali parallele del disegno, mentre il punto $R$ è il punto di distanza, ossia il punto dove si incontrano le linee a 45° dell'immagine originale. Ora il punto esatto da cui osservare il quadro, per riprodurre l'effetto, si trova sulla verticale al piano del disegno passante per il punto $P$, ad un'altezza pari a $\overline{PR}$ ¹. Pertanto stabilendo a priori la distanza $\overline{EP}$ a cui vogliamo posizionarci dal quadro, l'altezza $\overline{PR}$ da cui vogliamo osservare il quadro, e la lunghezza $\overline{FE}$ del disegno, possiamo ricavare le misure del lato inferiore e superiore dello stesso.

Poniamo:

$\overline{EP}=a$ $\overline{PR}=b$ $\overline{FE}=c$

Vogliamo calcolare $\overline{AD}$ e $\overline{CB}$. Indichiamo $\overline{AF}$ con $x$. I triangoli rettangoli $AFP$ e $BEP$ sono simili. Pertanto i cateti sono in proporzione tra loro. Si ha:

$\overline{AF}:\overline{FP}=\overline{BE}:\overline{EP}\quad\Rightarrow\quad x:(a+c)=\overline{BE}:a\quad\Rightarrow\quad \overline{BE}=\displaystyle\frac{ax}{a+c}$

Consideriamo ora i triangoli rettangoli $ARG$ e$ ACI$. Sono anch'essi simili, quindi i cateti sono in proporzione tra loro:

$\overline{IC}:\overline{AI}=\overline{GR}:\overline{AG}\quad\Rightarrow\quad (\overline{IE}+\overline{EC}):c=(\overline{GP}+\overline{PR}):(\overline{AI}+\overline{IG})\quad\Rightarrow\quad$ $\displaystyle \left(x+\frac{ax}{a+c}\right):c=(x+b):(a+c)\quad\Rightarrow\quad ax+cx+ax=cx+bc$

e dunque $\displaystyle x=\frac{bc}{2a}$ , ossia $\overline{AF}=x=\displaystyle\frac{bc}{2a}$.

Di conseguenza

$\overline{AD}=2\overline{AF}=\displaystyle\frac{bc}{a}$

$\overline{BC}=2\overline{EB}=\displaystyle 2\frac{ax}{a+c}=\displaystyle 2\frac{a\frac{bc}{2a}}{a+c}=\displaystyle\frac{bc}{a+c}$

Pertanto, ricapitolando, una volta impostata la distanza dal quadro $a$, l'altezza del punto di osservazione $b$ e la lunghezza del quadro $c$, ricaviamo le misure dei lati inferiore e superiore del disegno attraverso le seguenti:

$\displaystyle\overline{AD}=\frac{bc}{a}\qquad\qquad\displaystyle\overline{BC}=\frac{bc}{a+c}$

Nel nostro caso abbiamo scelto la distanza dal quadro pari a $4,50\;mt$, l'altezza da terra pari a $1,70\;mt$ (altezza "media" di una persona) e la lunghezza complessiva del disegno pari a $9\;mt$, ottenendo:

$\displaystyle\overline{AD}=\frac{1,7\cdot 9}{4,5}=3,4\;mt$

$\displaystyle\overline{BC}=\frac{1,7\cdot 9}{4,5+9}=1,1\overline{3}\;mt$

Dopo di che, con un programma di fotoritocco abbiamo deformato il disegno secondo i valori sopra calcolati, e mandato il tutto in stampa!

RIFERIMENTI BIBLIOGRAFICI

• Jean François Niceron, La perspective curieuse, ou magie artificielle des effets merveilleux de l'optique par la vision directe… Parigi, 1638 (disponibile qui)
• Paolo Di Lazzaro, Daniele Murra, l'anamorfosi tra arte, percezione visiva e "prospettive bizzarre"  Roma, 2013 (disponibile qui)
• Paolo Di Lazzaro, Daniele Murra, Pietro Vitelli, Calcolo analitico del punto di osservazione nelle anamorfosi prospettiche. Dimostrazione dell'assioma di Nicéron  Roma, 2015 (disponibile qui)