Anamorfosi - Il tassello mancante

Bene, lo scorso anno ci eravamo lasciati con una anamorfosi floreale riuscita e con una dimostrazione incompleta delle formule per la realizzazione di un anamorfismo. Pertanto quest'anno ci è sembrato doveroso riprendere il discorso con un nuovo esperimento floreale, e con la dimostrazione "completa" del procedimento anamorfico.

Veniamo dapprima all'esperimento floreale, con un pò di fotografie che documentano la riuscita dell'effetto (e anche qualche imprecisione "anamorfica" :) ). Per la cronaca il gruppo di "sbandati" è sempre il solito, con l'aggiunta di una new entry!

Formule parametriche per la realizzazione di una anamorfosi obliqua

Consideriamo la seguente costruzione geometrica:

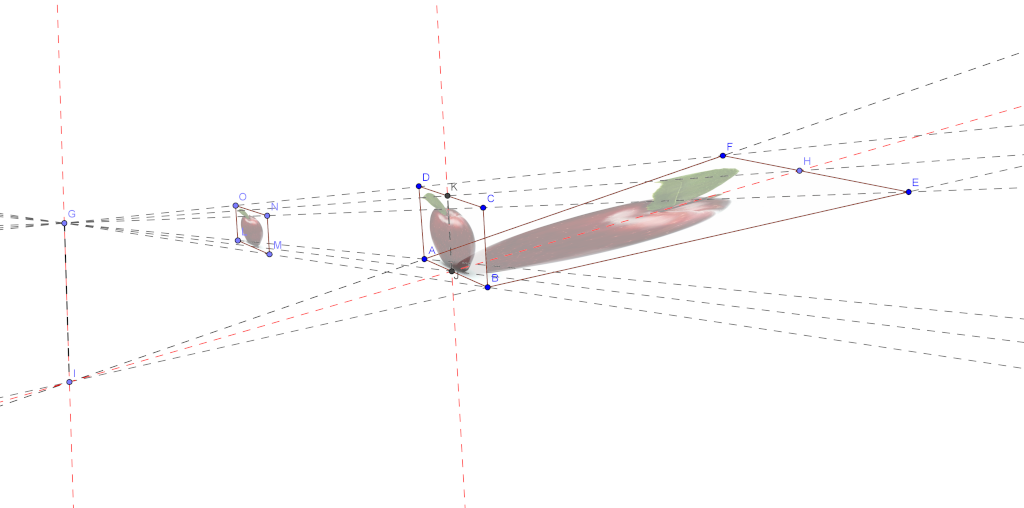
Il punto $G$ è il nostro punto di osservazione. Le rette passanti per $G$ rappresentano le linee prospettiche. Il quadrilatero $ABFE$ è il nostro disegno anamorfico (deformato) da realizzare. I rettangoli $LMNO$ e $ABCD$ invece rappresentano il disegno originale, ovvero quello che  l'osservatore vedrà dal punto di osservazione $G$. Il piano del rettangolo $ABCD$ è perpendicolare al piano del trapezio $ABEF$. Il punto $I$ si trova sul piano del trapezio $ABEF$, sulla perpendicolare al segmento $AB$ passante per il suo centro $J$. Il punto $G$ invece si trova sulla perpendicolare al piano del trapezio $ABEF$, passante per $I$. Ora essendo la proiezione in figura assimilabile ad una prospettiva centrale, con $G$ punto di proiezione, ed avendo supposto i segmenti $AB$ e $CD$ paralleli (rettangolo $ABCD$), allora i segmenti $AB$ ed $FE$ sarannno anch'essi paralleli. Pertanto sul piano del trapezio $ABEF$, la perpendicolare ad $\overline{AB}$ passante per il centro $J$, passa anche per il centro $H$ del segmento $\overline{FE}$. Consideriamo come parametri iniziali la lunghezza $\overline{JH}$ del quadro, la distanza $\overline{IJ}$ dell'osservatore dal quadro, l'altezza $\overline{IG}$ del punto di osservazione, e la larghezza inferiore $\overline{AB}$ del quadro. Pertanto poniamo:

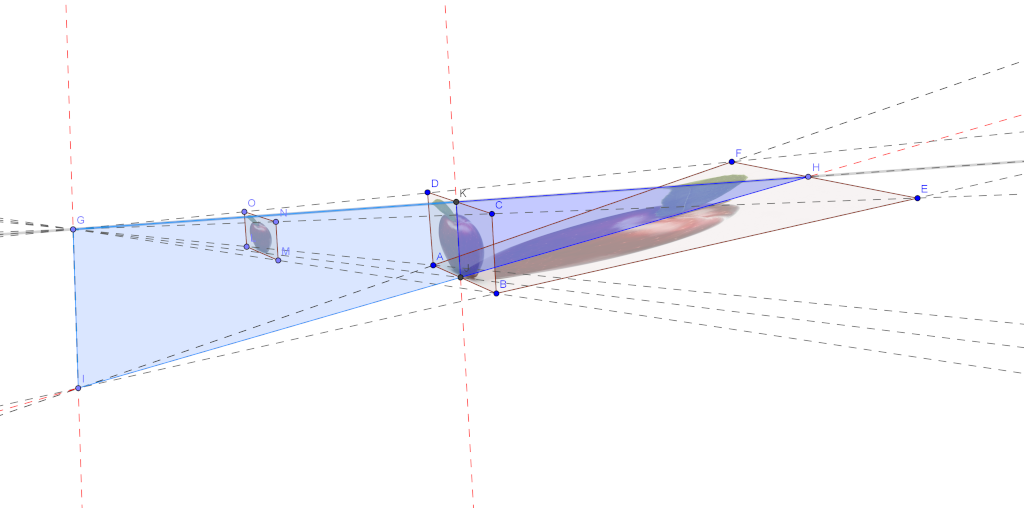
$\overline{IJ} = a$ $\overline{IG} = b$ $\overline{JH} = c$ $\overline{AB} = d$

Consideriamo ora i 2 triangoli $IHG$ e $JHK$ (vedi figura su). Essi sono triangoli rettangoli e simili, in quanto hanno i 3 angoli congruenti. Pertanto i cateti sono in proporzione tra loro. Si ha:

$\overline{IG}:\overline{IH}=\overline{JK}:\overline{JH}\quad\Rightarrow\quad b:(a+c)=\overline{JK}:c\quad\Rightarrow\quad \overline{JK}=\displaystyle\frac{bc}{a+c}$

Si noti come l'altezza $\overline{JK}$ del disegno originale sia determinata univocamente dalla lunghezza $\overline{JH}$ del quadro, dalla distanza $\overline{IJ}$ dell'osservatore da esso, e dall'altezza $\overline{IG}$ del punto di osservazione.

Calcoliamo ora il lato superiore $\overline{EF}$ del quadro. Poniamo $\overline{FE} = x$. Consideriamo i 2 triangoli $FIE$ e $AIB$ (vedi figura sotto).

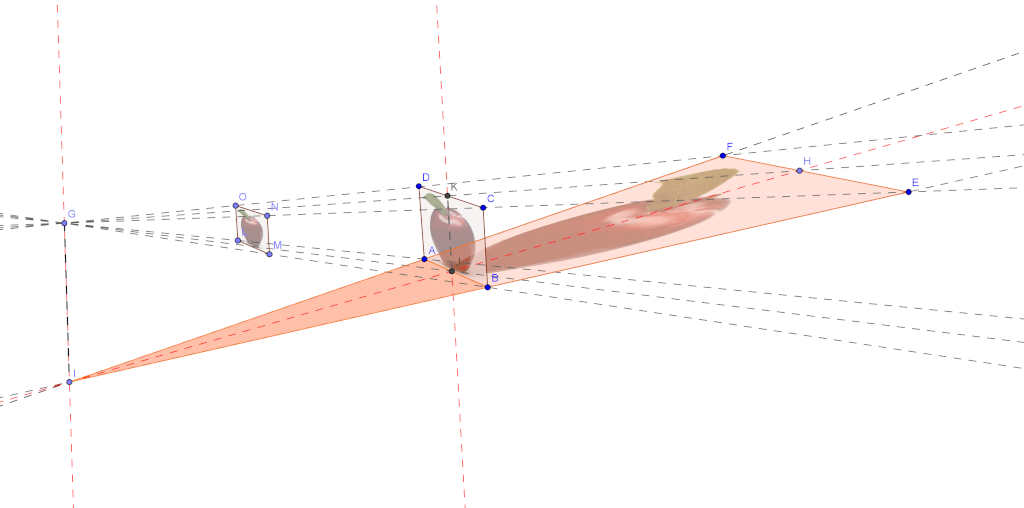
Essi sono isosceli e simili dal momento che $\overline{AB}$ ed $\overline{FE}$ sono paralleli, ed il punto $I$ si trova sulla perpendicolare ad essi passante per il loro centro. Per cui possiamo mettere in proporzione i cateti alla base con le altezze:

$\overline{FE}:\overline{AB}=\overline{IH}:\overline{IJ}\quad\Rightarrow\quad x:(a+c)=d:a\quad\Rightarrow\quad x=\displaystyle\frac{d(a+c)}{a}$

Dunque $\overline{FE}=\displaystyle\frac{d(a+c)}{a}$

Pertanto, ricapitolando, una volta impostata la distanza dal quadro $a$, l'altezza del punto di osservazione $b$, la lunghezza del quadro $c$, e la larghezza inferiore del quadro $d$, abbiamo che le misure dell'altezza $\overline{BC}$ del disegno originale, e del lato superiore $\overline{FE}$ del quadro valgono:

$\displaystyle\overline{BC}=\frac{bc}{a+c}\qquad\qquad\displaystyle\overline{FE}=\displaystyle\frac{d(a+c)}{a}$

Considerazioni sul metodo di costruzione proposto da J.Niceron

Il matematico francese Jean François Niceron è stato uno dei maggiori studiosi dell'anamorfosi, e ci ha lasciato molti dettagli sulle costruzioni anamorfiche nella sua Perspective curieuse. Di particolare interesse per l'anamorfosi obliqua sono le due figure XXXVIII e XXXIX del trattato:

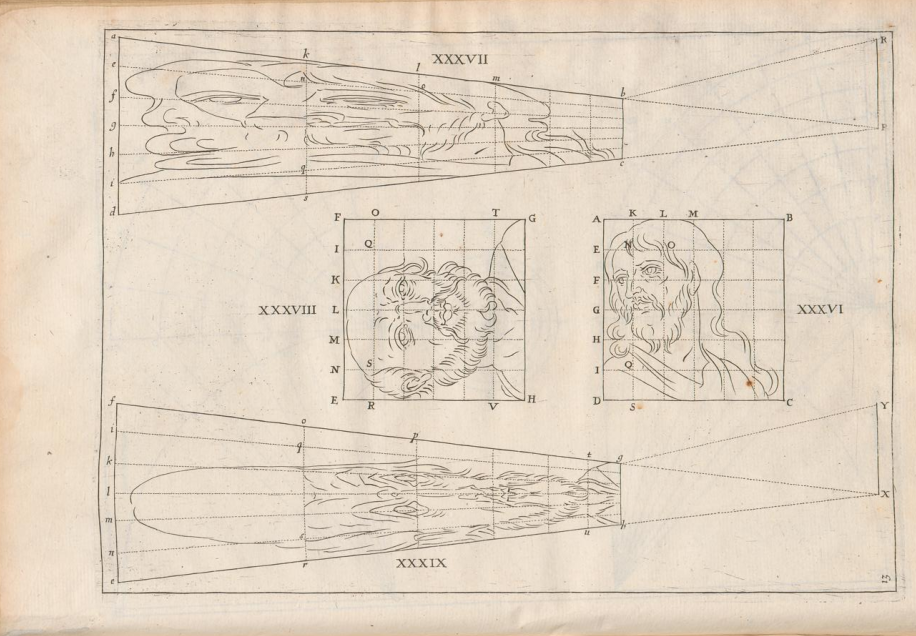
Per maggiore chiarezza consideriamo la seguente versione equivalente della costruzione di Niceron:

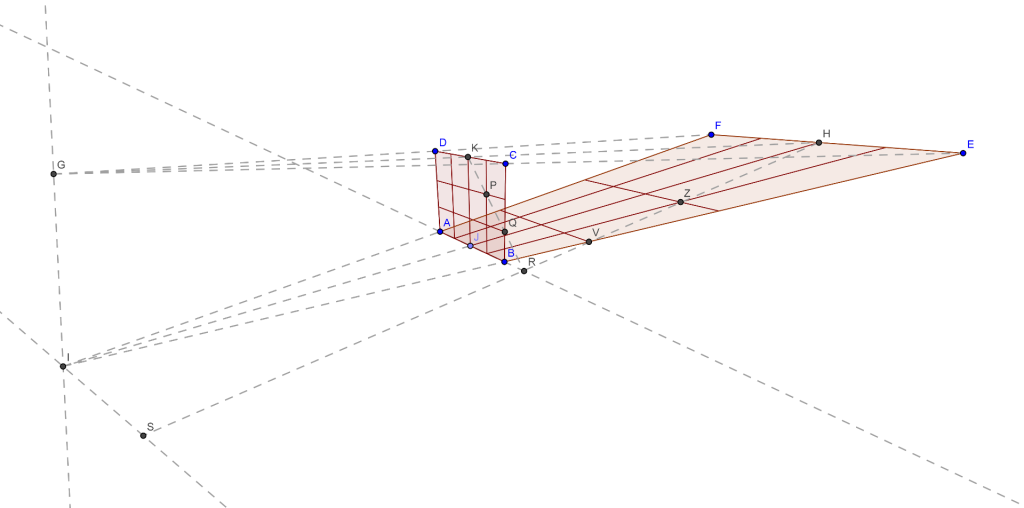
Niceron fa coincidere il punto di osservazione del quadro anamorfico con il punto di distanza ¹ dello stesso. Dunque l'altezza da cui osservare il quadro per apprezzare l'effetto anamorfico risulta essere uguale alla distanza tra il punto di fuga $I$ del quadro e il punto di distanza $S$ dello stesso. Ora, come già scritto in altro post, ciò trova immediato riscontro pratico e l'effetto anamorfico riesce perfettamente, tuttavia una dimostrazione analitica manca. Pertanto, vediamo come dimostrare questa equivalenza.

Partiamo dalla costruzione in figura 2 ad inizio post e prendiamo in considerazione la retta a 45° del disegno originale, passante per $K$, ossia per il centro del lato $CD$ del rettangolo $ABCD$. Otteniamo la seguente:

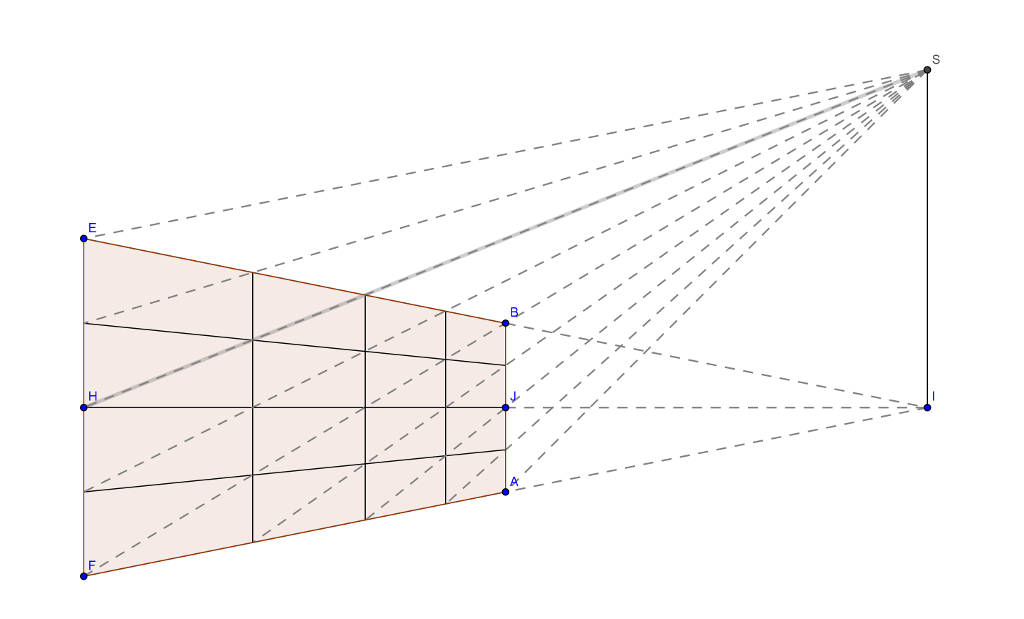
dove, sia il disegno originale $ABCD$ che il corrispettivo anamorfico $ABEF$ sono stati suddivisi in quadratini, come nella costruzione di Niceron, per permettere il tracciamento delle linee a 45° di interesse. La retta $HS$ del quadro anamorfico corrisponde alla retta $KR$ del disegno originale. Da notare che la posizione del punto $R$ dipende dalle dimensioni del disegno originale; nel nostro caso, essendo il quadrilatero $ABCD$ un rettangolo, il punto $R$ si trova oltre il segmento $\overline{AB}$. Si tratta di dimostrare che $\overline{IS}=\overline{IG}$.

Poniamo, come sopra: $\overline{IJ} = a$ $\overline{IG} = b$ $\overline{JH} = c$ $\overline{AB} = d$ Ora consideriamo i due triangoli rettangoli $IHS$ e $JHR$. Essi sono simili, in quanto aventi tre angoli uguali. Per cui possiamo mettere in proporzione i cateti alla base con le altezze. Si ha:

$\overline{IH}:\overline{JH}=\overline{IS}:\overline{JR}\quad\Rightarrow\quad (a+c):c=\overline{IS}:\overline{JR}$

Essendo la retta $KR$ a 45° rispetto alle rette verticali ed orizzontali del rettangolo $ABCD$, si ha che il triangolo $JRK$ risulta rettangolo ed isoscele. Quindi $JR$ risulta uguale a $JK$ ossia all'altezza del disegno originale, che abbiamo dimostrato essere uguale a $\displaystyle\frac{bc}{a+c}$. Sostituendo nella proporzione si ha: $(a+c):c=\overline{IS}:\displaystyle\frac{bc}{a+c}$ da cui $\overline{IS}=\displaystyle\frac{(a+c)\displaystyle\frac{bc}{a+c}}{c}=b$

Dunque $\overline{IS}=\overline{IG}$.

P.S.: Ringrazio il Dr. Di Lazzaro ed il Dr. Murra dell'ENEA per la disponibilità e per avermi segnalato errori ed inesattezze nelle mie considerazioni.

Aggiornamento: la scrittura di questo articolo, ha dato seguito ad una collaborazione proposta l'anno precedente dal Dr. Di Lazzaro e dal Dr. Murra, con la quale si è giunti alla pubblicazione dell'ENEA dal titolo "Calcolo analitico del punto di osservazione nelle anamorfosi prospettiche. Dimostrazione dell'assioma di Nicéron".
E' possibile leggere e/o scaricare la pubblicazione da QUI.

RIFERIMENTI BIBLIOGRAFICI

• Jean François Niceron, La perspective curieuse, ou magie artificielle des effets merveilleux de l'optique par la vision directe… Parigi, 1638 (disponibile qui)
• https://it.wikipedia.org/wiki/Prospettiva