Origami - Costruzione di una molecola in tassellazioni "Flagstone"

In geometria piana, con il termine tassellazione (o anche "tassellatura") si indica la copertura del piano con una o più figure geometriche (dette appunto "tasselli") ripetute all'infinito, senza sovrapposizioni e senza spazi tra esse.
Analogamente, nel mondo origami, vengono chiamate tassellazioni tutti quei modelli formati da "tasselli" uguali (o anche simili) che si ripetono nel piano.
Ogni tassellazione viene sempre realizzata da un unico foglio di carta opportunamente piegato.
A differenza delle tassellazioni geometriche, i tasselli possono essere sia piani che tridimensionali.

Tassellazioni "Flagstone"

Le tassellazioni origami possono essere suddivise in vari sottogruppi, ognuno con caratteristiche peculiari.
Uno di questi sottogruppi è quello delle tassellazioni flagstone.
Si tratta di tassellazioni nelle quali i bordi dei tasselli che la compongono sono adiacenti e sullo stesso piano, senza sovrapposizioni.
Ricordano le pavimentazioni a "pietre piatte", da qui il nome "flagstone" in lingua inglese.
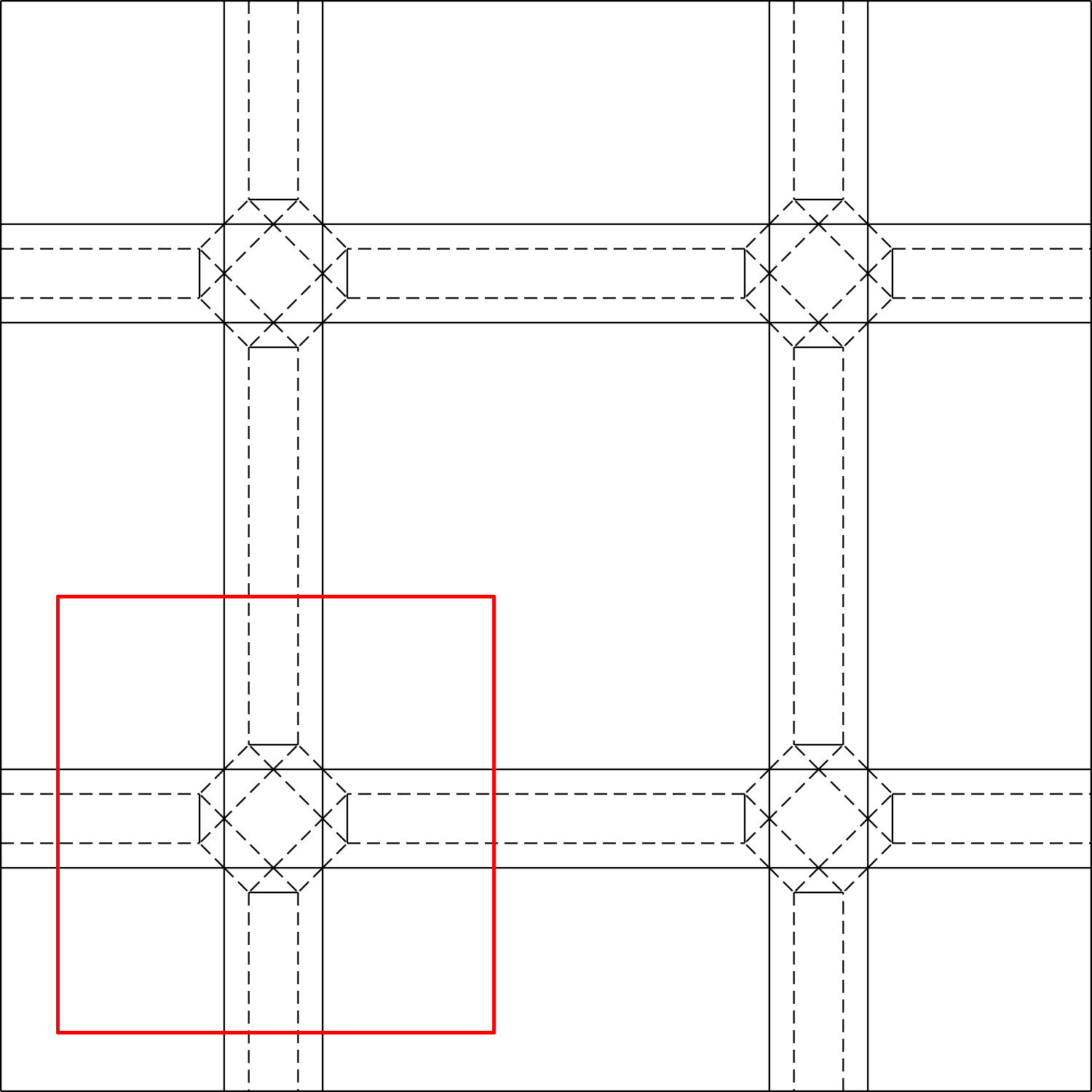
Nella figura di seguito vi sono alcuni esempi di queste tassellazioni.

Tecniche note

La tecnica più popolare nella realizzazione di tassellazioni flagstone è probabilmente quella proposta da Eric Gjerde nel suo libro Origami Tessellations ¹.
Questa tecnica consiste nel prepiegare il nostro foglio secondo una griglia quadrata o triangolare.
Dopo di che si cominciano ad esplorare possibili pattern per tassellazioni flagstone piegando lungo le prepieghe effettuate all'inizio.
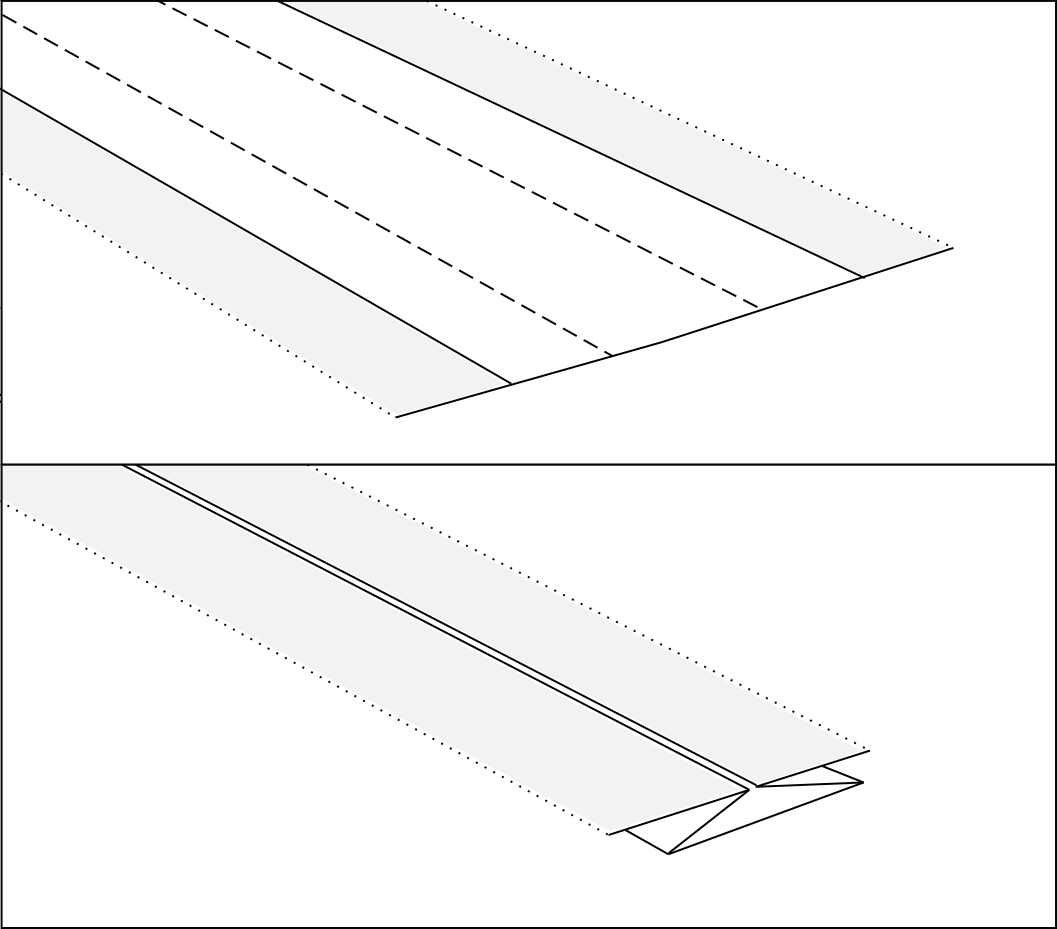
In fig.2 vi sono un esempio di foglio prepiegato, ed una tassellazione flagstone ottenuta da tale foglio.
La spiegazione e illustrazione di tale tecnica sarebbe troppo lunga da farsi qui, ed esula da quello che è lo scopo dell'articolo.
Pertanto vi rimando al suddetto libro Origami Tessellations, contenente la spiegazione dettagliata e visuale di varie tecniche di tassellazione, nonchè illustrazioni commentate, passo dopo passo, per la realizzazione di molteplici modelli a partire da un foglio prepiegato secondo griglie.

Una tecnica più generale, è la costruzione geometrica proposta da Robert J. Lang nel suo libro Twists, Tilings and Tessellations ².
Lang dedica diverse pagine alle tassellazioni Flagstone, partendo dalle condizioni matematiche necessarie affinchè una tassellazione flagstone sia realizzabile e piegabile, quindi fornendo un algoritmo geometrico per la costruzione di un generico nodo della tassellazione.
Di seguito viene illustrata una possibile costruzione geometrica utilizzando una versione modificata di tale algoritmo, che ne semplifica l'applicazione.

Molecole e costruzione geometrica

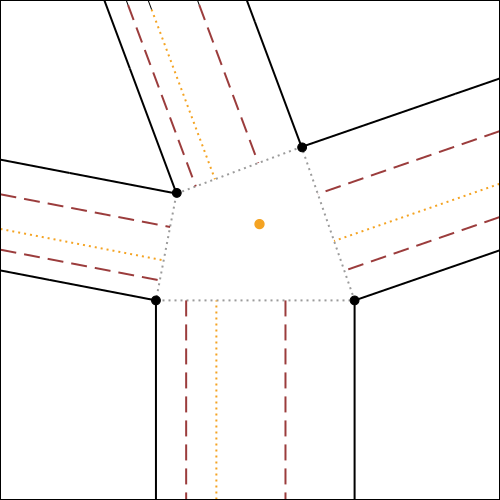
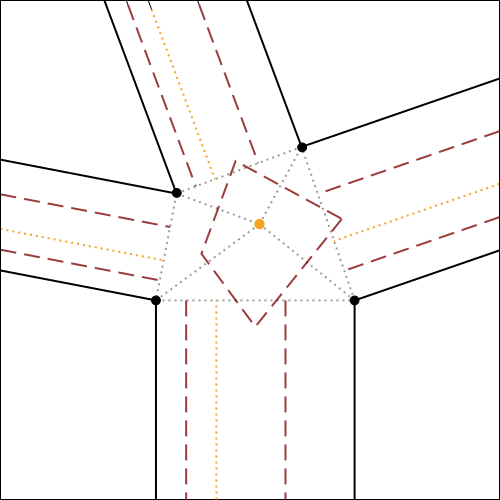
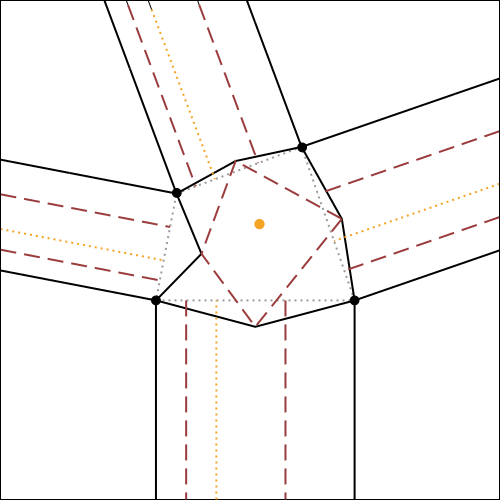
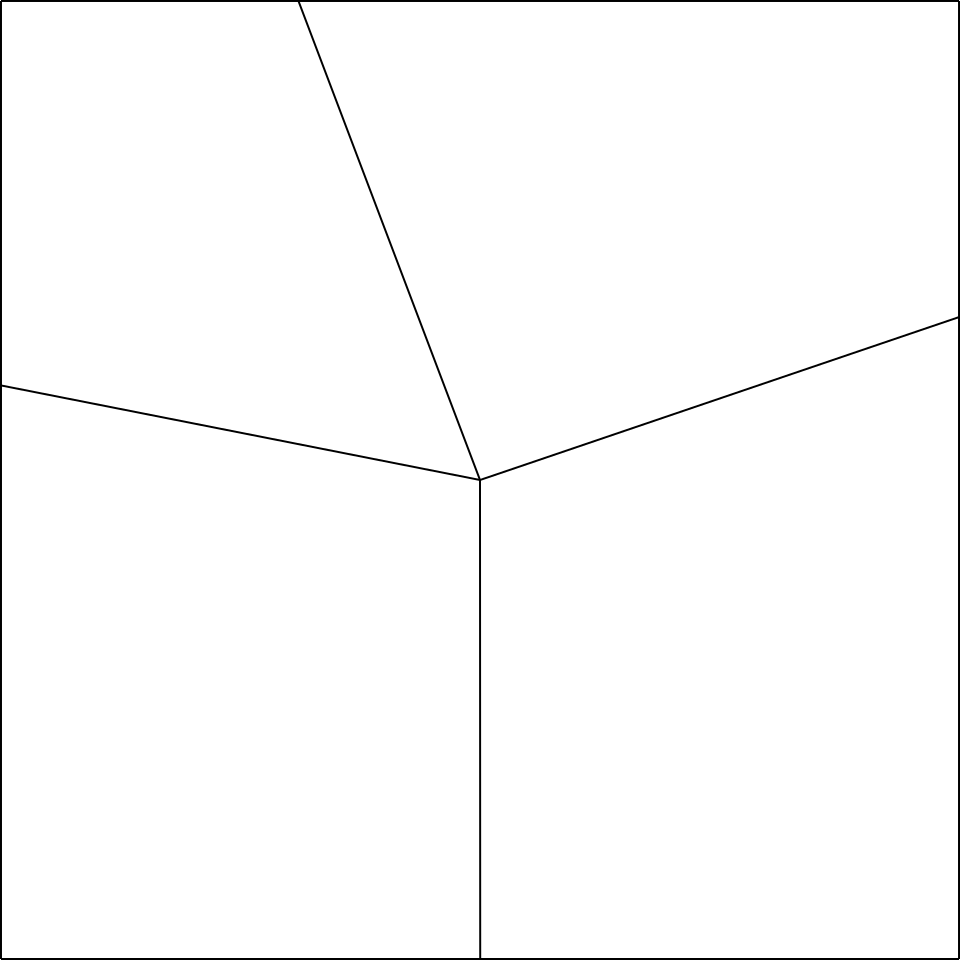
Consideriamo un nodo qualsiasi di un modello finito di tassellazione (fig.3a); la parte corrispondente al nodo, nel crease pattern iniziale (fig.3b e 3c) viene detta comunemente molecola della tassellazione.

I rettangoli di carta, invece, corrispondenti alle linee che formano il nodo, li chiameremo "strisce" del nodo.
Bene, vediamo prima come determinare tali strisce di carta rettangolari tra i poligoni, per poi passare alla costruzione della molecola relativa.

Costruzione delle strisce

Dunque, iniziamo col dire che le "strisce" di carta tra i poligoni, costituiscono l'eccesso di carta che, quando piegato, ci permette di far combaciare gli spigoli dei poligoni adiacenti, per formare il nodo finale con effetto flagstone (vedi fig.4).

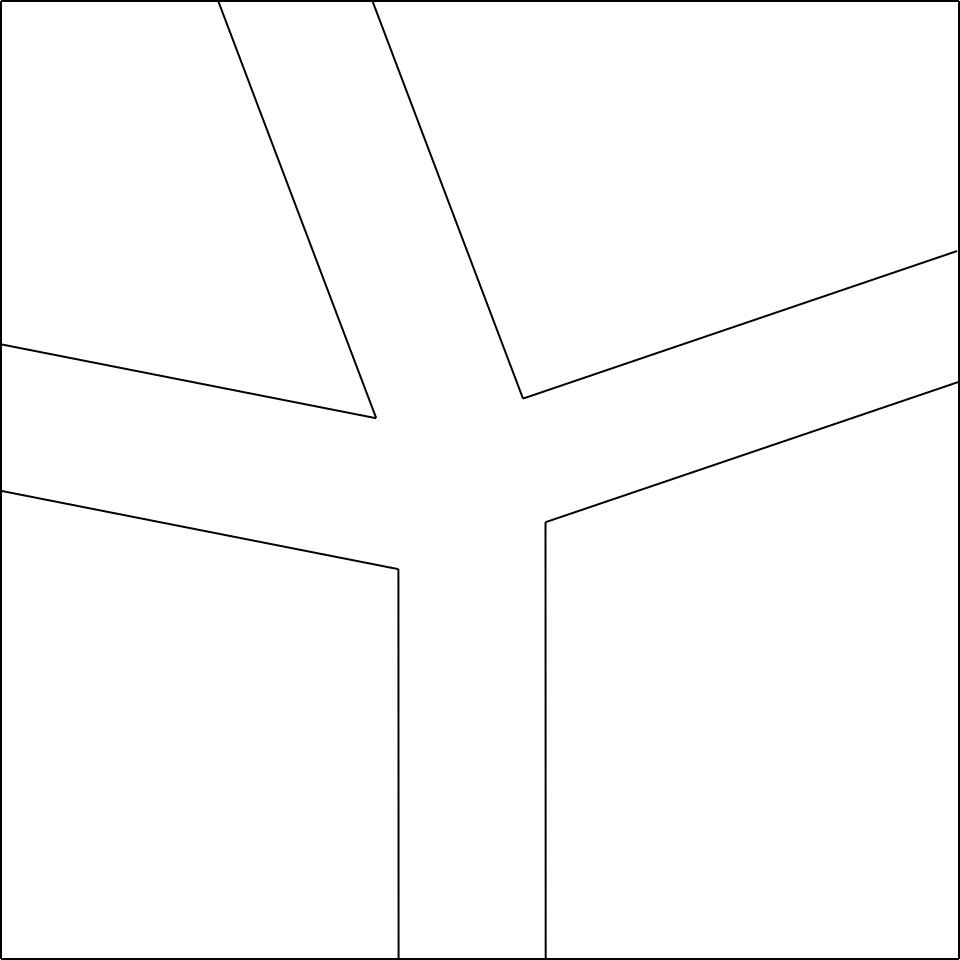
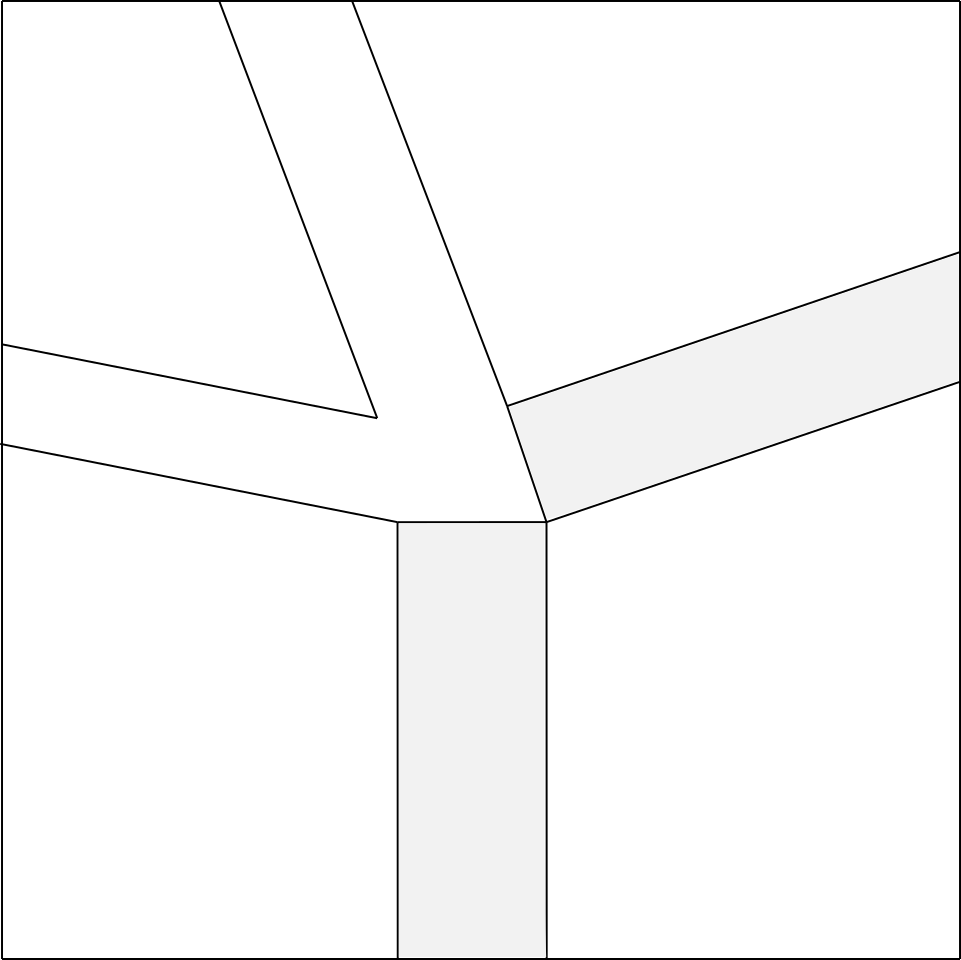
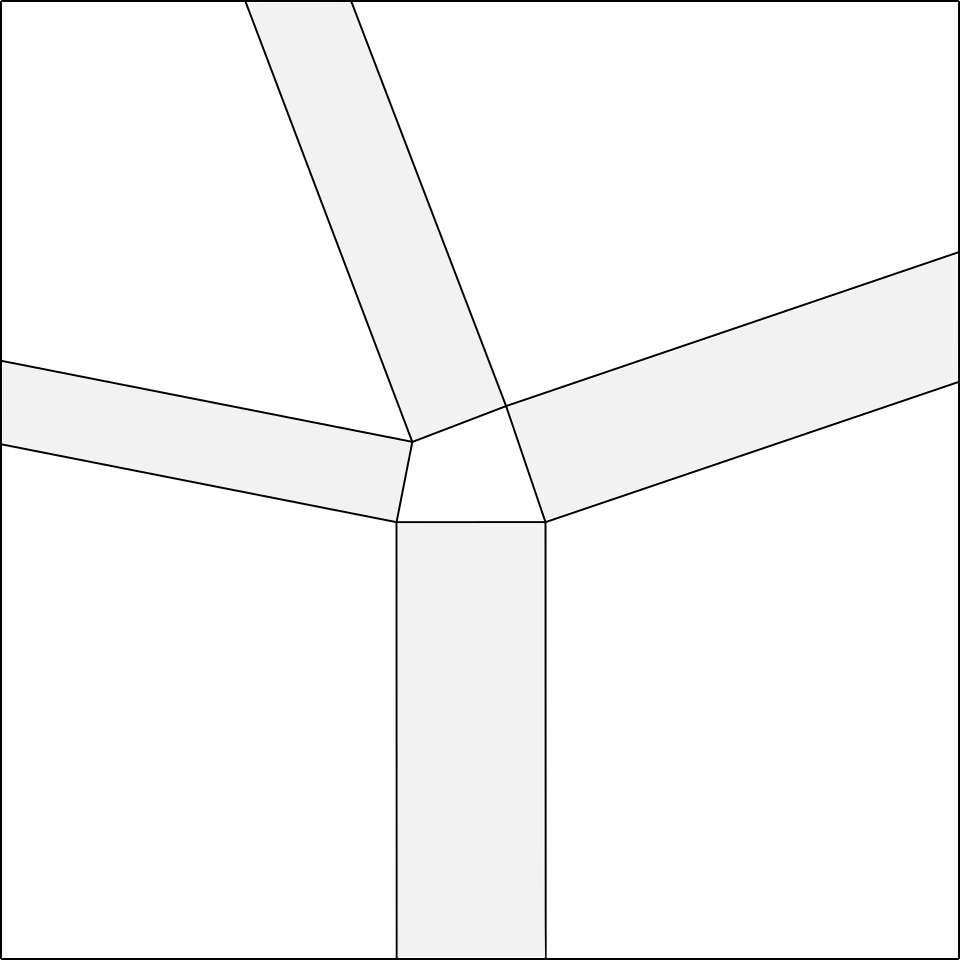
Premesso ciò, partiamo dal nodo che si vuole ottenere (prendiamo ad esempio il nodo in fig.5a).
Immaginiamo di aprire il nodo in questione (fig.5b), e aggiungiamo un rettangolo di larghezza piccola a piacere ³ tra i due poligoni in basso, ed un rettangolo tra i due poligoni a destra (fig.5c).
A questo punto, i restanti due rettangoli da aggiungere, avranno una larghezza obbligata, determinata dal loro punto di incontro, che sarà il vertice del poligono in alto a sinistra, come mostra la fig.5d.

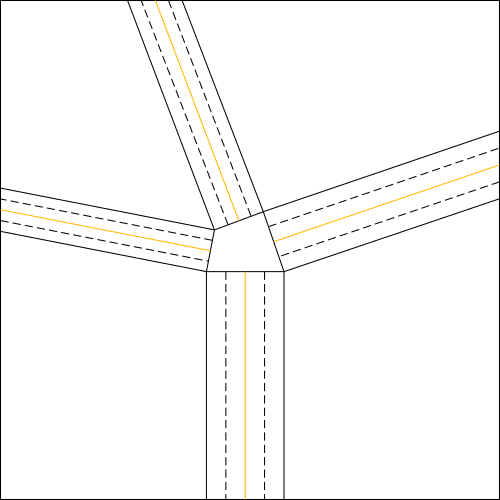
Una volta determinate le strisce del nodo, tracciamo le due linee interne a ciascuna striscia, parallele ai lati lunghi della stessa, necessarie per effettuare la doppia piega (fig.4).
A seconda della posizione in cui si vuol far convergere la doppia piega, le due linee verranno scelte ad una specifica distanza dai lati paralleli della striscia;
in particolare, verranno scelte ad una distanza che è a metà tra la linea di convergenza (linee in arancio in fig.6) e il relativo lato parallelo.
Il prossimo passo è quello di determinare la molecola delimitata da tali strisce.

Costruzione della molecola

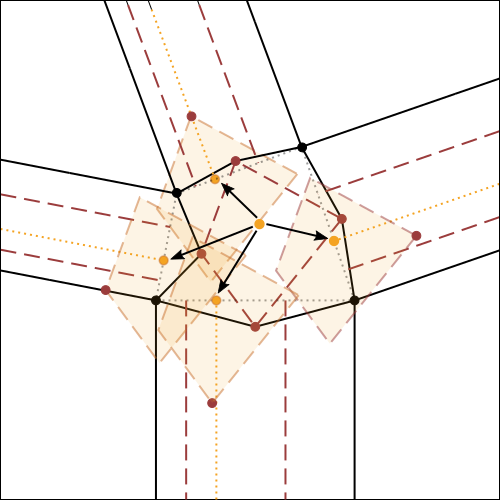
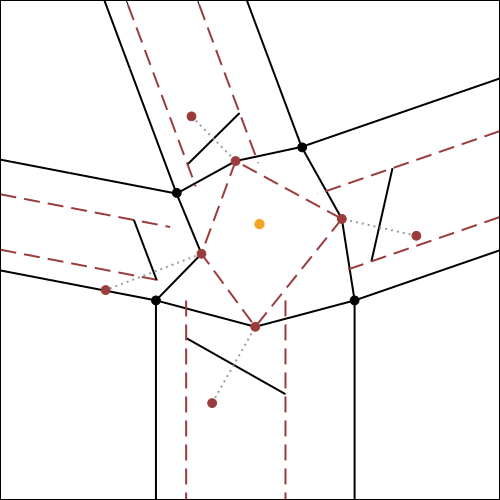
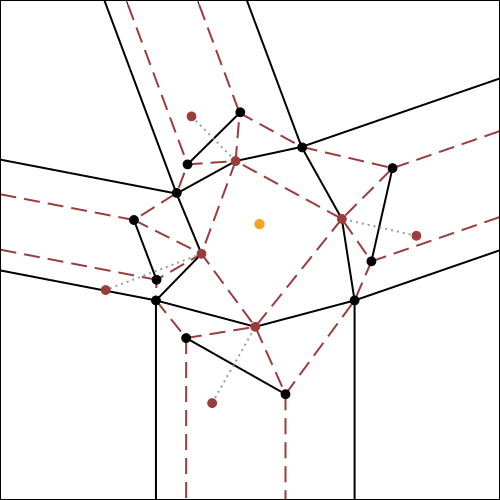
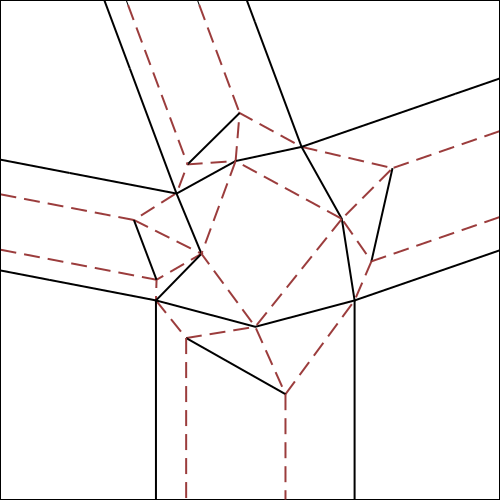
Nella fig.7 che segue, viene illustrato e spiegato esaustivamente l'algoritmo per la costruzione della molecola ⁴, utilizzando come riferimento iniziale il crease pattern della fig.6.
E' possibile cliccare su ogni step per ingrandirlo.

Tale algoritmo si presta bene ad essere utilizzato nei software di disegno vettoriale (come ad es. inkscape), mentre è più complicato utilizzarlo direttamente su carta.

Nella figura seguente (fig.8) è riportato un esempio pratico di utilizzo di tale algoritmo.

Calcolo analitico

Partendo dal crease pattern finale valido di una molecola, possiamo utilizzare la geometria analitica per calcolare i valori dei punti di interesse e dei segmenti del crease pattern, in funzione dei dati iniziali noti.
Analizziamo di seguito il caso di una molecola a 4 rami (4 strisce).
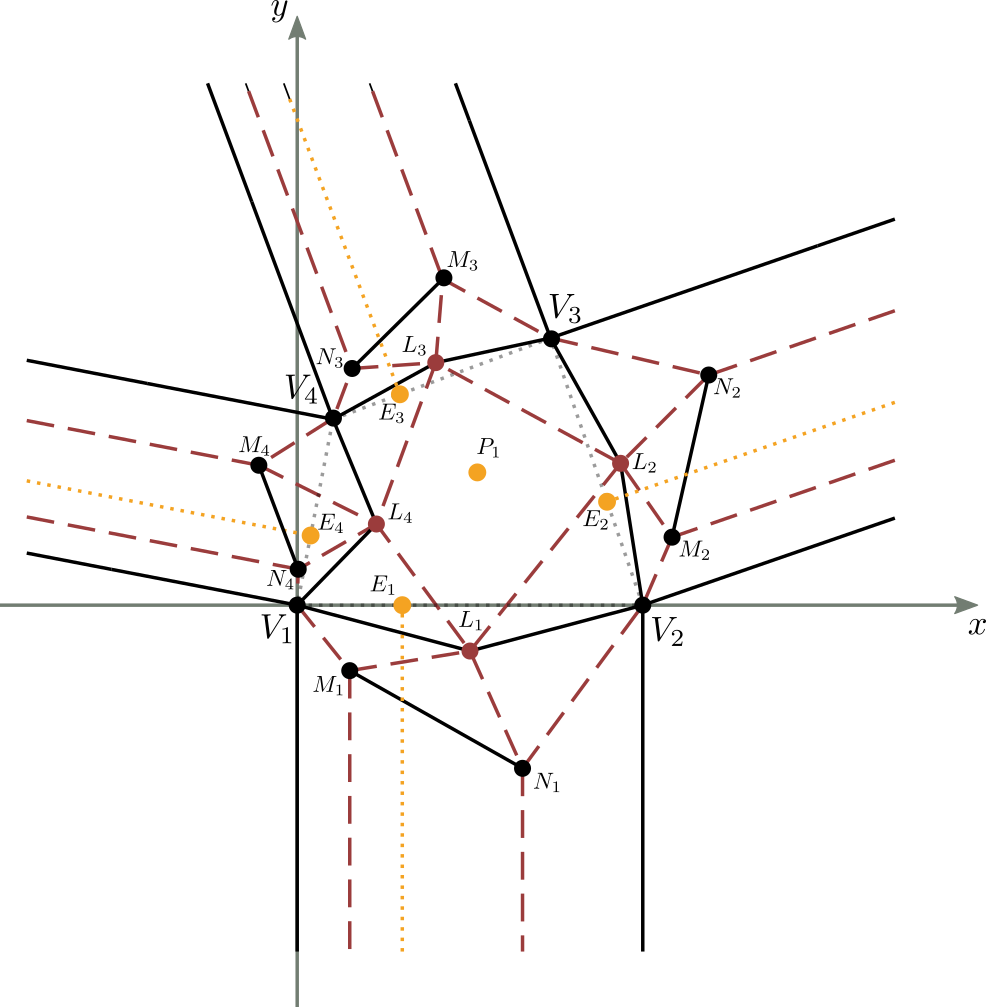
Consideriamo la figura 9 in cui viene riportato sul piano cartesiano un crease pattern completo e valido di una molecola, con il primo vertice della parte centrale coincidente con il centro di origine degli assi del piano, e la base della parte centrale giacente sull'asse delle ascisse.
I dati iniziali noti, sono in sostanza la forma e dimensione della parte centrale della molecola (il quadrilatero $V_1V_2V_3V_4$ in figura), definita completamente da 3 dei suoi angoli e 2 dei suoi lati, la posizione del centro $P_1$ all'interno della parte centrale, e il punto di convergenza $E_i$ della doppia piega per ciascuna striscia $i$, con $1 \leq i \leq 4$.
Pertanto, poniamo, per comodità:

$\hat{V_4V_1V_2} = \alpha_1$, $\quad\hat{V_1V_2V_3} = \alpha_2$, $\quad\hat{V_2V_3V_4} = \alpha_3$
$\overline{V_1V_2} = \ell_1$, $\quad\overline{V_2V_3} = \ell_2$, $\quad P_1(P_{1x}, P_{1y})$
$\overline{V_1E_1}=c_1$, $\quad \overline{V_2E_2}=c_2$, $\quad \overline{V_3E_3}=c_3$, $\quad \overline{V_4E_4}=c_4$

con $\alpha_1$, $\alpha_2$, $\alpha_3$, $\ell_1$, $\ell_2$, $P_{1x}$, $P_{1y}$ e $c_1$, $c_2$, $c_3$, $c_4$ noti.

I valori $\alpha_1$, $\alpha_2$ e $\alpha_3$ sono vincolati al fatto che $V_1V_2V_3V_4$ sia un quadrilatero convesso.
$\ell_1$ e $\ell_2$ sono maggiori di zero.
$P_{1x}$ e $P_{1y}$ sono vincolati al fatto che il punto $P_1$ cada all'interno del quadrilatero $V_1V_2V_3V_4$.
I valori $c_1$, $c_2$, $c_3$ e $c_4$ sono positivi, compresi tra 0 e la larghezza delle relative strisce.

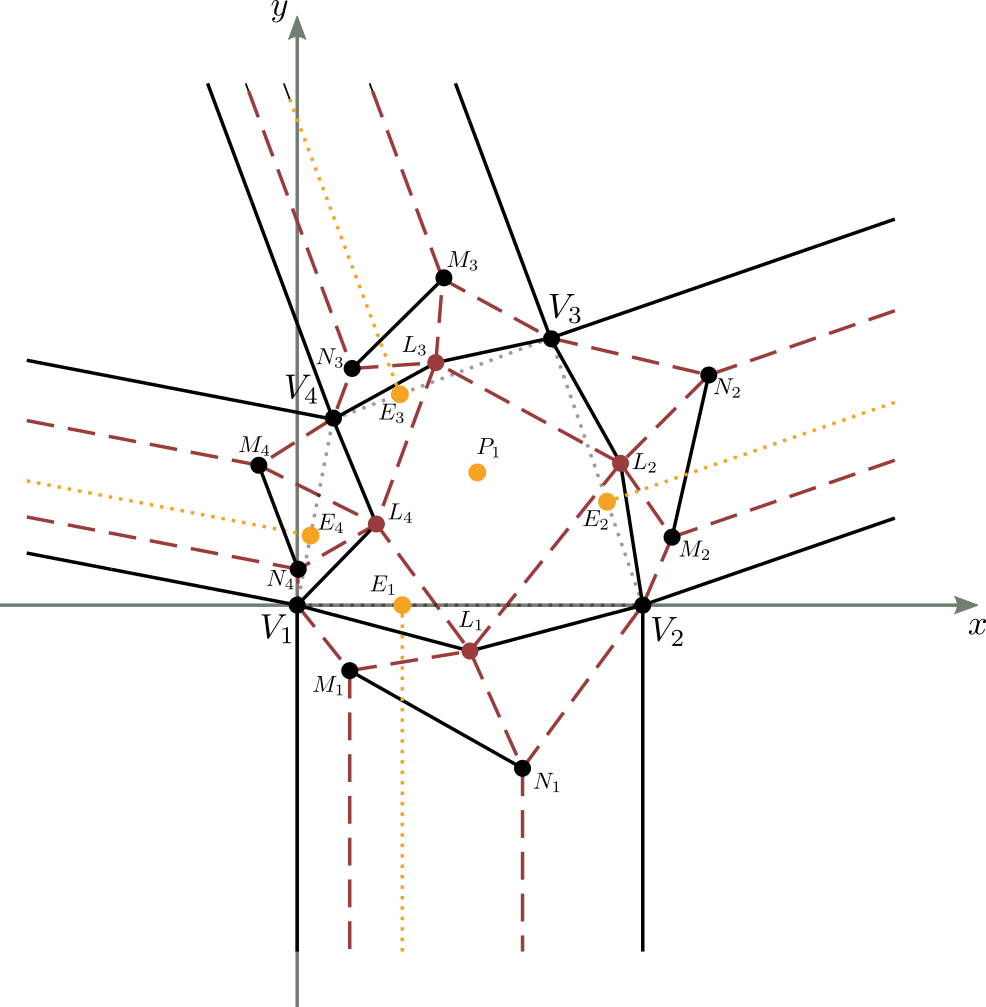
Osservando la figura, si nota che per poter disegnare univocamente il crease pattern è necessario conoscere la posizione dei punti $L_i$, $M_i$ ed $N_i$ di ciascuna striscia $i$, con $1\le i \le 4$.
Iniziamo calcolando i valori dei punti $P_1$, $M_1$ e $N_1$ della prima striscia.

Calcolo valori della prima striscia

Utilizziamo la successiva figura (fig.10), che è un ingrandimento della figura 9, incentrato solo sulla prima striscia, esteso con tutti i passaggi intermedi della costruzione geometrica di figura 7.

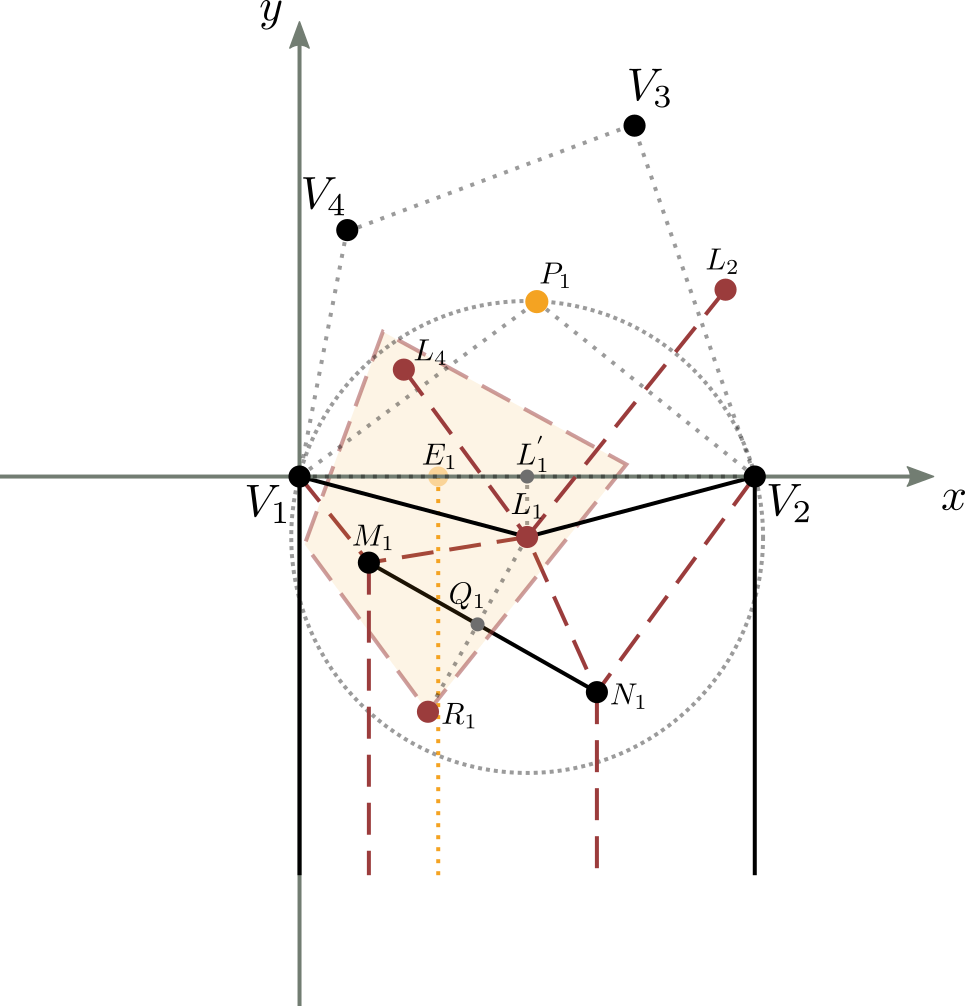
Avendo scelto, per comodità, il punto $V_1$ coincidente con l'origine degli assi e il segmento $\overline{V_1V_2}$ giacente sull'asse delle $x$, ne segue che le coordinate dei punti $V_1$ e $V_2$ valgono:

$V_1(0,0)$ e $V_2(\ell_1,0)$

Ora, dalla geometria del triangolo sappiamo che il punto di intersezione degli assi dei lati di un triangolo qualsiasi, coincide con il circocentro, ossia con il centro della circonferenza circoscritta a tale triangolo.
Dal momento che i segmenti $\overline{L_{4}L_{1}}$ e $\overline{L_{1}L_{2}}$ sono gli assi dei segmenti $\overline{P_1V_1}$ e $\overline{P_1V_2}$, allora il punto $L_1$ risulta essere il circocentro del triangolo $\overset{\Delta}{V_1V_2P_1}$.
Quindi l'ascissa del punto $L_1$, essendo l'asse del segmento $\overline{V_1V_2}$ passante per $L_1$, vale $\displaystyle L_{1x} = \frac{\overline{V_1V_2}}{2} = \frac{\ell_1}{2}$.

Per calcolare l'ordinata del punto $L_1$ invece, possiamo considerare il fatto che $\overline{V_1L_1}$, $\overline{V_2L_1}$ e $\overline{P_1L_1}$ sono raggi della circonferenza circoscritta al triangolo $\overset\Delta{V_1V_2P_1}$;
in particolare si ha $\overline{V_1L_1}=\overline{P_1L_1}$.
Ponendo pertanto $\overline{L_1^{'}L_1} = L_{1y} = y$, si ha:

quindi

Calcoliamo ora $R_1$.
Essendo, per costruzione, $\overline{L_1R_1} = \overline{P_1E_1}$, allora:

ossia

Calcoliamo $Q_1$.
Essendo $Q_1$, per costruzione, il punto medio di $\overline{L_1R_1}$, si ha:

ossia

Calcoliamo ora $M_1$ ed $N_1$, facendo riferimento alla figura 11 di seguito.

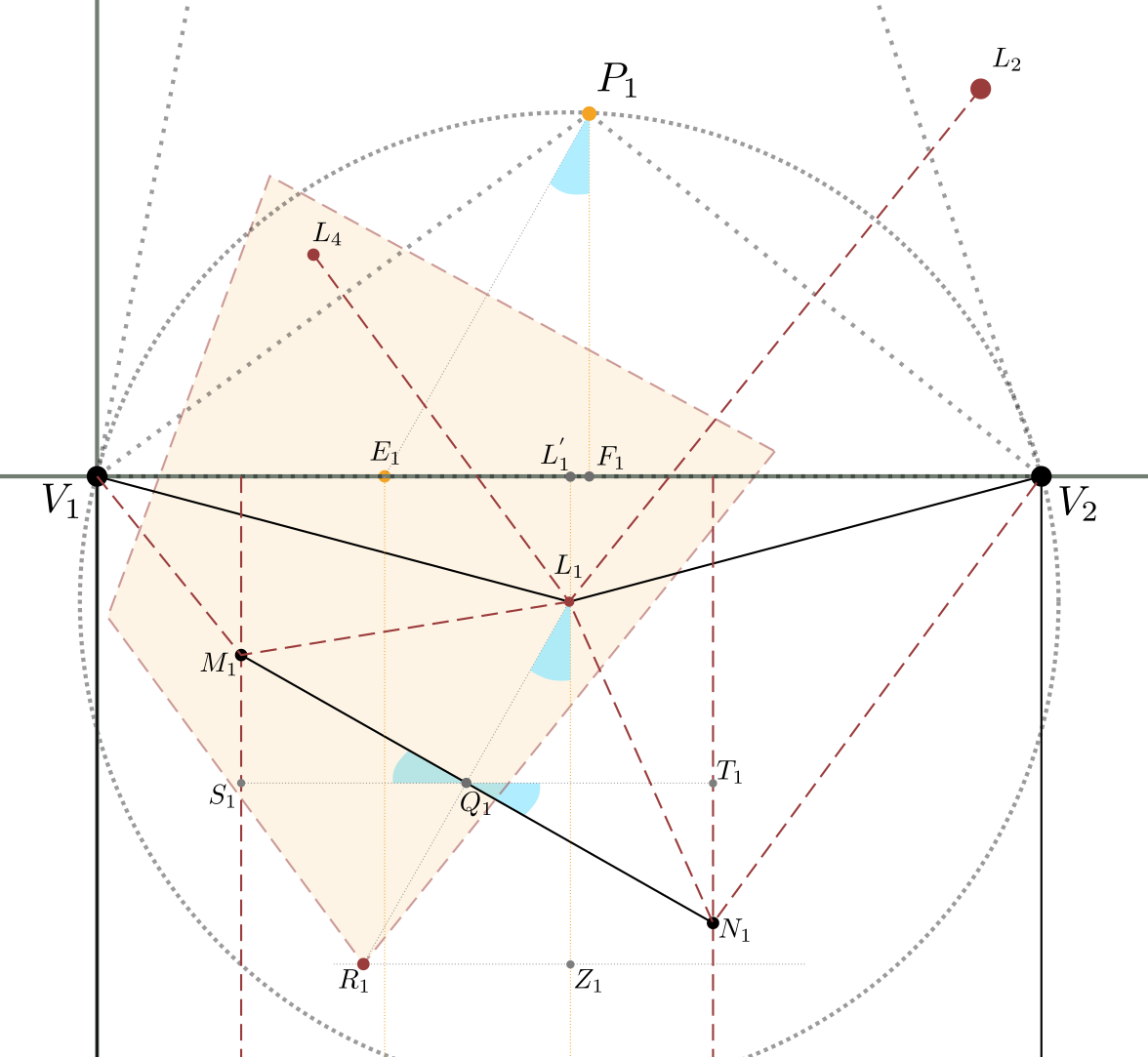
Consideriamo il segmento $\overline{S_1Q_1}$ perpendicolare a $\overline{L_1Z_1}$ e parallelo a $\overline{V_1V_2}$.
Essendo anche, per la costruzione iniziale, $\overline{M_1N_1}$ perpendicolare a $\overline{L_1R_1}$, e $\overline{L_1R_1} = \overline{P_1E_1}$, si ha che gli angoli in azzurro segnati in figura sono tutti uguali; ossia

Calcoliamo ora $M_1$.
L'ascissa di $M_1$ è già nota per costruzione e vale $\displaystyle M_{1x} = \frac{\overline{V_1E_1}}{2} = \frac{c_1}{2}$ .
L'ordinata invece ci è data da:

Dato che, come visto sopra, $ \small\hat{S_1Q_1M_1} = \small\hat{E_1P_1F_1}$, sostituendo si ha:

Sostituendo infine i valori $Q_{1x}$, $Q_{1y}$ e $M_{1x}$ trovati in precedenza, si ha:

ossia

Calcoliamo infine $N_1$, utilizzando un ragionamento analogo a quanto fatto per $M_1$.

L'ascissa di $N_1$ vale $\displaystyle N_{1x} = \frac{E_{1x}+V_{2x}}{2} = \frac{c_1+\ell_1}{2}$ .
L'ordinata invece ci è data da:

Dato che, come visto sopra, $ \small\hat{T_1Q_1N_1} = \small\hat{E_1P_1F_1}$, sostituendo si ha:

Sostituendo infine i valori $Q_{1x}$, $Q_{1y}$ e $N_{1x}$ trovati in precedenza, si ha:

ossia

Quindi, ricapitolando, i punti di interesse per la costruzione del crease pattern, relativamente alla prima striscia (lato $\overline{V_1V_2}$ del quadrilatero) valgono:

Calcolo valori della seconda striscia

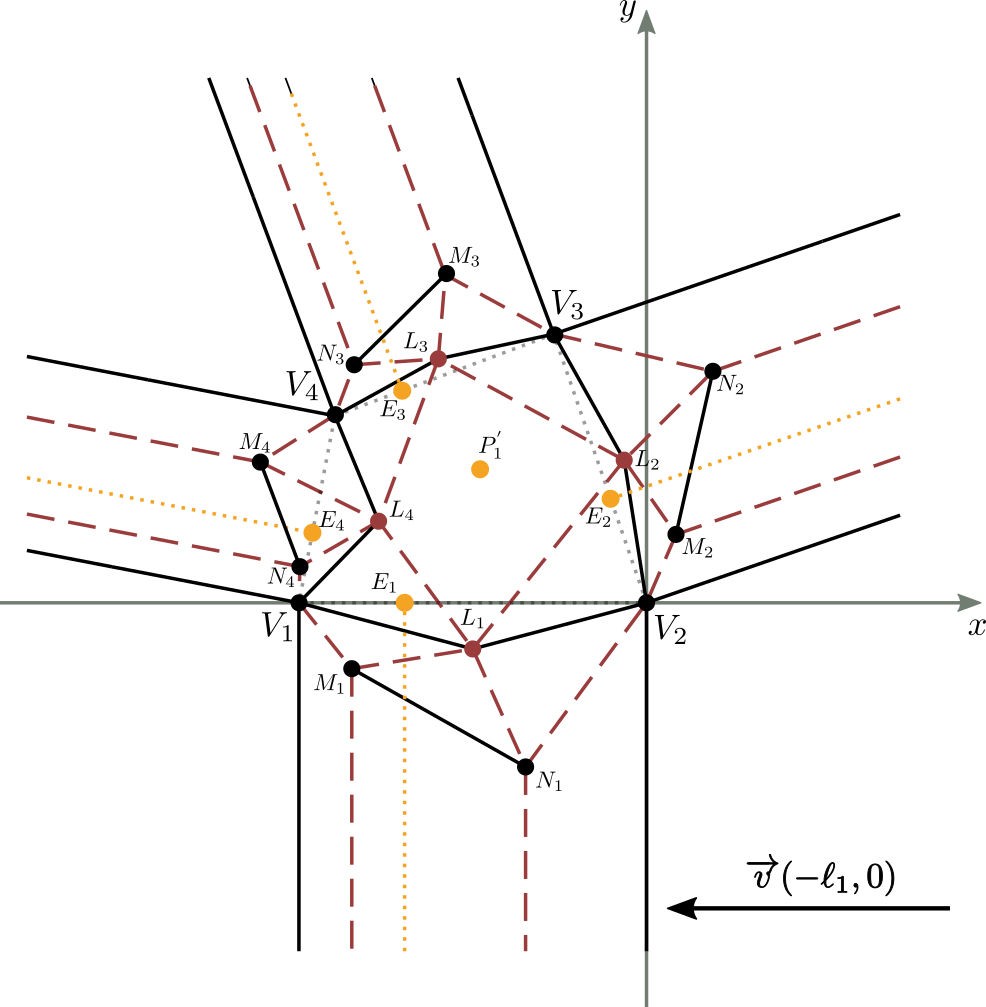
Per calcolare i valori $L_2$, $M_2$ e $N_2$ della seconda striscia (quella di lato $\overline{V_2V_3}$), possiamo immaginare di traslare e ruotare la molecola in modo tale che il punto $V_2$ coincida con l'origine degli assi e il segmento $\overline{V_2V_3}$ giaccia sull'asse delle ascisse (figura 12 ⁵).

La figura 12b mostra il risultato della traslazione della molecola di figura 12a, di vettore $\overrightarrow{v}(-\ell_1,0)$. Le equazioni di tale traslazione valgono:

dove $x$ e $y$ sono le coordinate note di un punto nel piano, mentre $x^{'}$ e $y^{'}$ sono le coordinate del suo trasformato, a seguito della traslazione.
Nello specifico calcoliamo le coordinate del punto $P^{'}_1$, trasformato di $P_1$ secondo la suddetta traslazione. Si ha:

ossia $P^{'}_1(P_{1x} -\ell_1, P_{1y})$.

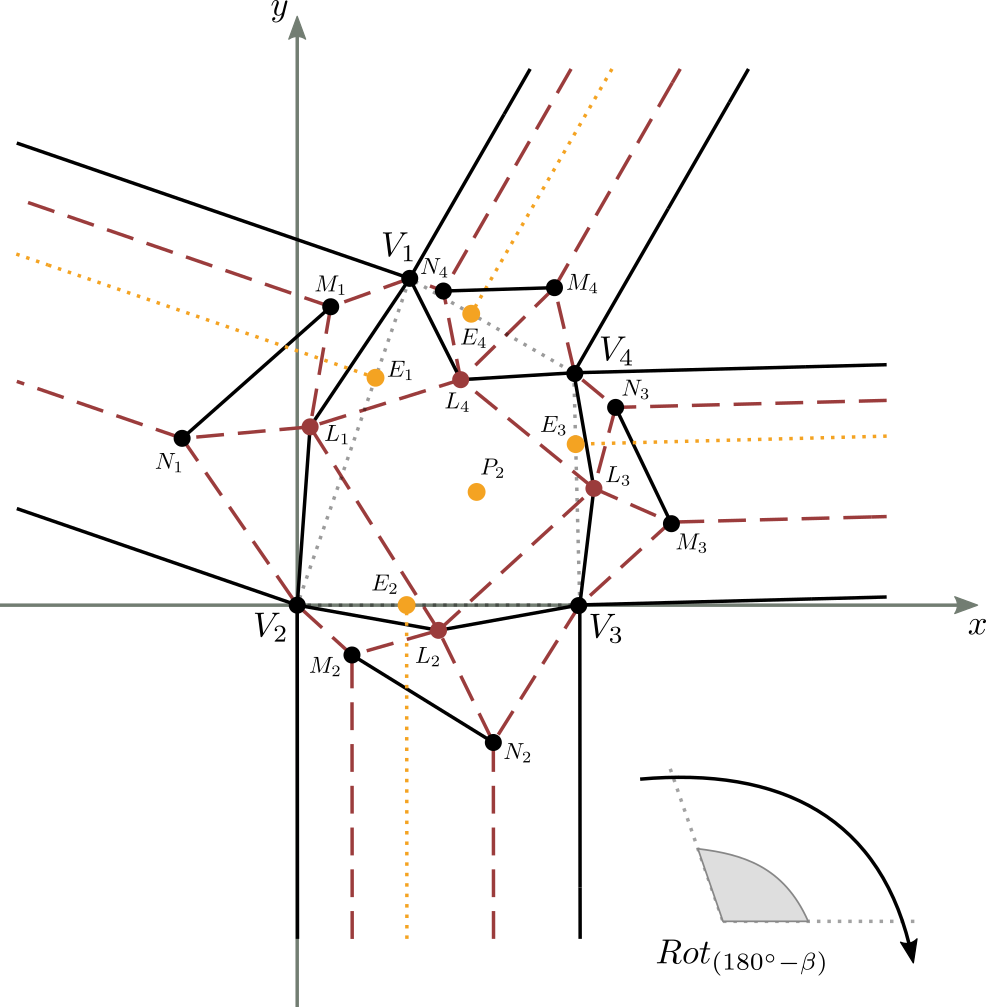
Applichiamo poi alla figura 12b un rotazione oraria intorno all'origine, di ampiezza pari a $180^{\circ} - \alpha_2$, al fine di avere $\overline{V_2V_3}$ giacente sull'asse $x$. Si ha:

dove $x$ e $y$ sono le coordinate note di un punto nel piano, mentre $x^{'}$ e $y^{'}$ sono le coordinate del suo trasformato, a seguito della rotazione.
Nello specifico calcoliamo le coordinate del punto $P_2$, trasformato di $P^{'}_1$ secondo la suddetta rotazione. Si ha:

ossia $P_2(\enspace(\ell_1-P_{1x})\cdot\cos{\alpha_2} + P_{1y}\cdot\sin{\alpha_2}\enspace,\enspace(\ell_1-P_{1x})\cdot\sin{\alpha_2} - P_{1y}\cdot\cos{\alpha_2}\enspace)$

A questo punto possiamo procedere al calcolo dei valori $L_2$, $M_2$ e $N_2$ (figura 12c), utilizzando le stesse formule ricavate per la prima striscia (sottoparagrafo precedente).

Partiamo quindi dalla figura 12c, risultato delle trasformazioni sopra analizzate. I dati iniziali noti sono sempre gli stessi che abbiamo definito all'inizio di questo paragrafo, ad eccezione delle coordinate del punto $P_1$, che sono state trasformate nel punto $P_2$, a seguito delle due operazioni di traslazione e rotazione.
Pertanto abbiamo i seguenti dati:

$\quad\hat{V_1V_2V_3} = \alpha_2$
$\quad\overline{V_2V_3} = \ell_2$
$\quad P_2(\enspace(\ell_1-P_{1x})\cdot\cos{\alpha_2} + P_{1y}\cdot\sin{\alpha_2}\enspace,\enspace(\ell_1-P_{1x})\cdot\sin{\alpha_2} - P_{1y}\cdot\cos{\alpha_2}\enspace)$
$\quad \overline{V_2E_2}=c_2$

con $\alpha_2$, $\ell_2$, $P_{2x}$, $P_{2y}$ e $c_2$ noti.

Sostituendo ora $\ell_1$ con $\ell_2$, $c_1$ con $c_2$, e i valori di $P_1$ con quelli di $P_2$ nelle formule della $\eqref{a}$, otteniamo i valori $L_2$, $M_2$ e $N_2$ desiderati. Si ha:

con $P_2(\enspace(\ell_1-P_{1x})\cdot\cos{\alpha_2} + P_{1y}\cdot\sin{\alpha_2}\enspace,\enspace(\ell_1-P_{1x})\cdot\sin{\alpha_2} - P_{1y}\cdot\cos{\alpha_2}\enspace)$.

Calcolo valori della $n$-esima striscia (generalizzazione)

Possiamo applicare ricorsivamente le trasformazioni utilizzate nel calcolo dei valori per la seconda striscia, per determinare i valori di una generica striscia $n$.
Pertanto generalizziamo, calcolando i valori $L_n$, $M_n$ e $N_n$ della $n$-esima striscia.
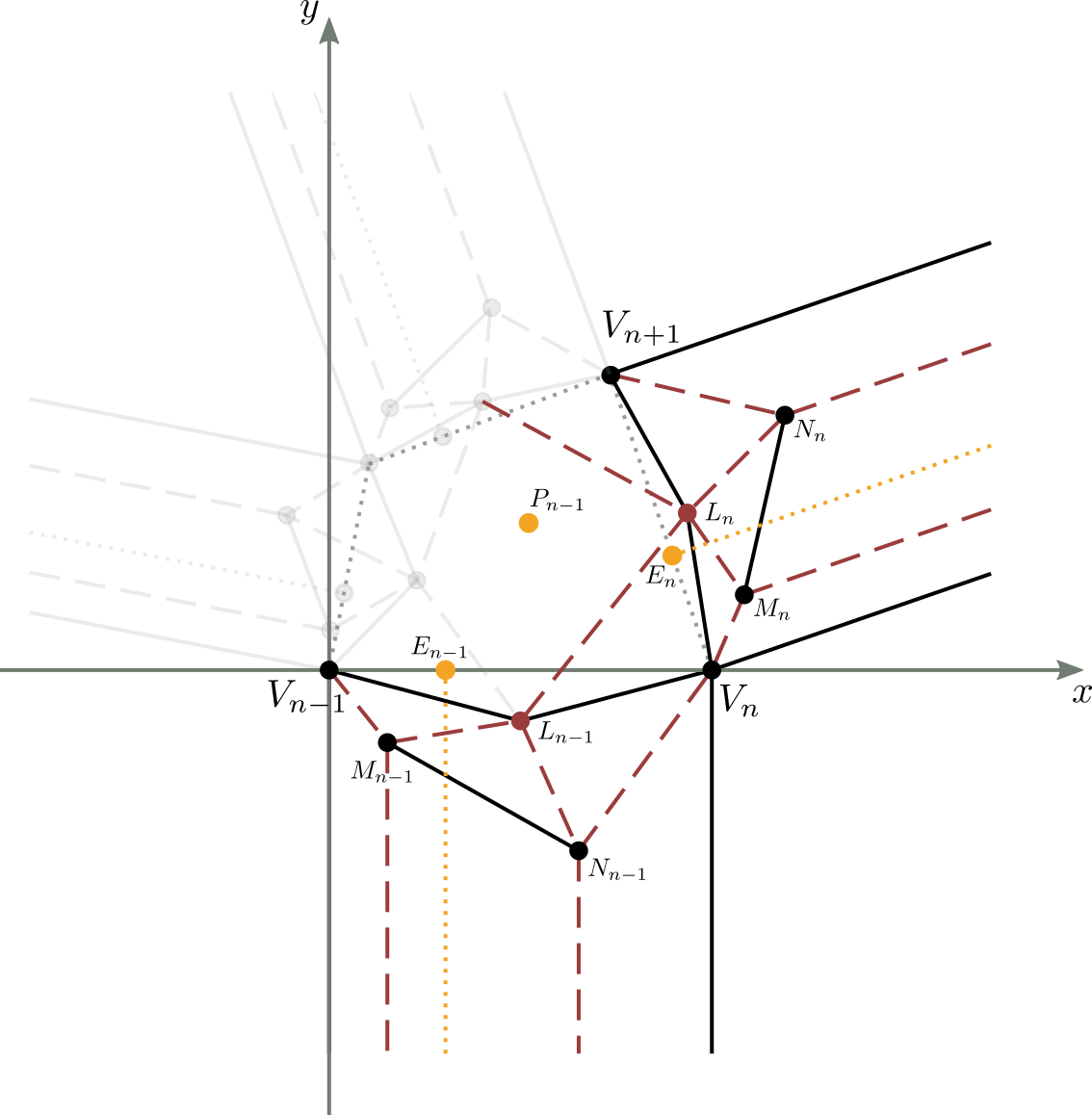
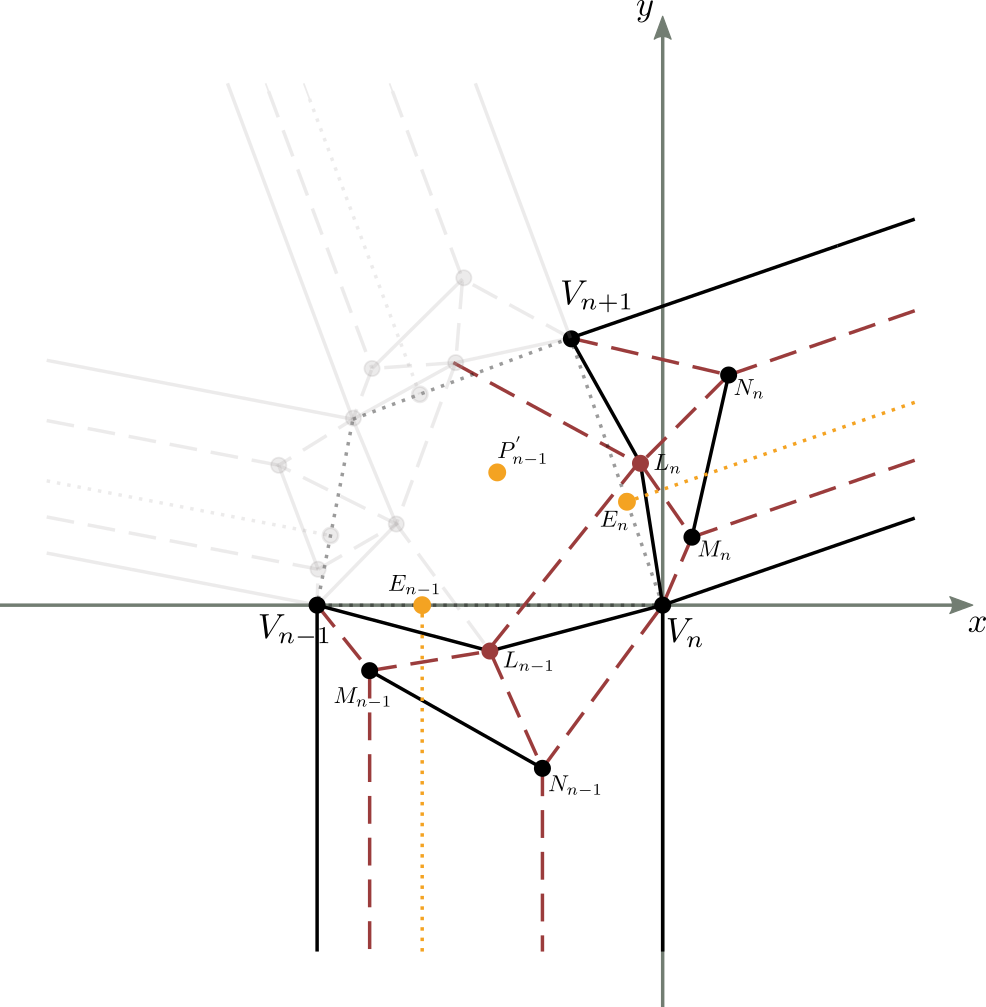
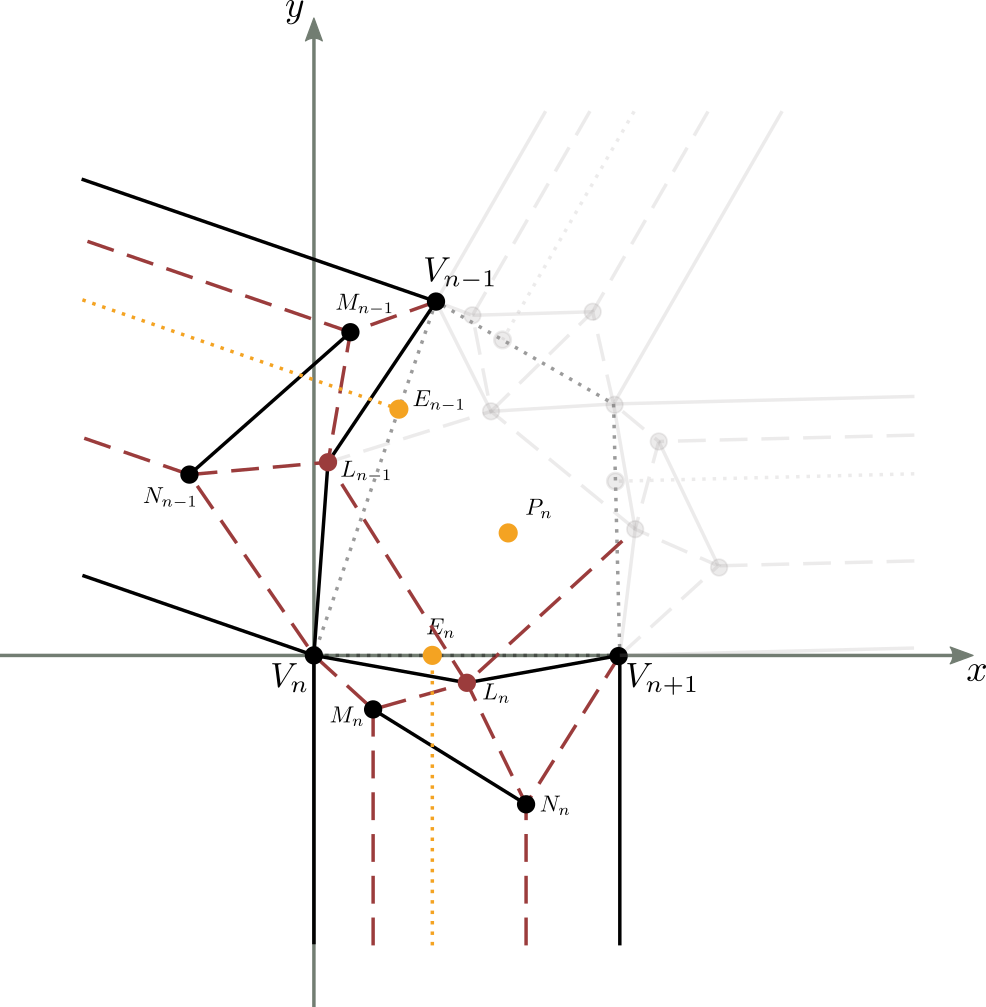
Consideriamo la figura 13a, che rappresenta una generica molecola, ed in particolare la sua striscia ($n$-1)-esima ed $n$-esima.
Applichiamo quindi una nuova traslazione e rotazione a questa molecola in modo tale che il punto $V_n$ coincida con l'origine degli assi (punto $V_{n-1}$) e il segmento $\overline{V_nV_{n+1}}$ giaccia sull'asse delle ascisse (figura 13c).

Per la traslazione di figura 13b si ha (analogamente a quanto visto già per la seconda striscia):

dove $x$ e $y$ sono le coordinate note di un punto nel piano, mentre $x^{'}$ e $y^{'}$ sono le coordinate del suo trasformato, a seguito della traslazione.
Nello specifico calcoliamo le coordinate del punto $P^{'}_{n-1}$, trasformato di $P_{n-1}$ secondo la suddetta traslazione. Si ha:

ossia $P^{'}_{n-1}(\enspace P_{n-1_{x}} -\ell_{n-1} \enspace,\enspace P_{n-1_{y}} \enspace)$.

Applichiamo poi alla figura 13b un rotazione oraria intorno all'origine, di ampiezza pari a $180^{\circ} - \alpha_n$, al fine di avere $\overline{V_nV_{n+1}}$ giacente sull'asse $x$. Si ha:

dove $x$ e $y$ sono le coordinate note di un punto nel piano, mentre $x^{'}$ e $y^{'}$ sono le coordinate del suo trasformato, a seguito della rotazione.
$\alpha_n$ invece è l'angolo del poligono centrale, di vertice $V_n$.
Nello specifico calcoliamo le coordinate del punto $P_n$, trasformato di $P^{'}_{n-1}$ secondo la suddetta rotazione. Si ha:

Sostituendo i valori di $P^{'}_{n-1x}$ e $P^{'}_{n-1y}$ ricavati dalla $\eqref{c1}$ si ha:

ossia $P_n(\enspace (\ell_{n-1}-P_{n-1_{x}})\cdot\cos{\alpha_n} + P_{n-1y}\cdot\sin{\alpha_n} \enspace,\enspace (\ell_{n-1}-P_{n-1_{x}}) \cdot\sin{\alpha_n} - P_{n-1y}\cdot\cos{\alpha_n} \enspace)$.

Procediamo dunque al calcolo dei valori $L_n$, $M_n$ e $N_n$, utilizzando sempre le formule della $\eqref{a}$.

Partiamo dalla figura 13c, risultato delle trasformazioni sopra analizzate.
I dati iniziali noti, in funzione di $n$, sono:

$\widehat{V_{n-1}V_nV_{n+1}} = \alpha_n$
$\overline{V_nV_{n+1}} = \ell_n$
$P_n(\enspace (\ell_{n-1}-P_{n-1_{x}})\cdot\cos{\alpha_n} + P_{n-1y}\cdot\sin{\alpha_n} \enspace,\enspace (\ell_{n-1}-P_{n-1_{x}}) \cdot\sin{\alpha_n} - P_{n-1y}\cdot\cos{\alpha_n} \enspace)$ $\overline{V_nE_n}=c_n$

con $\alpha_n$, $\ell_n$, $P_{nx}$, $P_{ny}$ e $c_n$ noti.

Sostituendo ora $\ell_1$ con $\ell_n$, $c_1$ con $c_n$, e i valori di $P$ con quelli di $P_n$ nelle formule della $\eqref{a}$, otteniamo i valori $L_n$, $M_n$ e $N_n$ desiderati. Si ha:

con $P_n(\enspace (\ell_{n-1}-P_{n-1_{x}})\cdot\cos{\alpha_n} + P_{n-1y}\cdot\sin{\alpha_n} \enspace,\enspace (\ell_{n-1}-P_{n-1_{x}}) \cdot\sin{\alpha_n} - P_{n-1y}\cdot\cos{\alpha_n} \enspace)$.

Conclusioni

Abbiamo dunque mostrato come costruire geometricamente, e come calcolare analiticamente molecole flagstone generiche (a $n$ rami), per realizzare tassellazioni di varia complessità.
Nello specifico, la costruzione geometrica risulta particolarmente utile per il disegno al computer della molecola, tramite software di grafica vettoriale come inkscape.
Il calcolo analitico, dal canto suo, ci fornisce le formule esatte che permettono di passare dai dati iniziali noti ai valori finali della molecola; cio' è stato fondamentale per la realizzazione di un software di calcolo/simuazione di molecole flagstone a $n$ rami, dove inserendo i dati iniziali desiderati, si ottiene in tempo reale il crease pattern della molecola cercata, con la possibilità di salvarlo in formato vettoriale.
Il software è descritto in questo articolo ed è disponibile su Github.